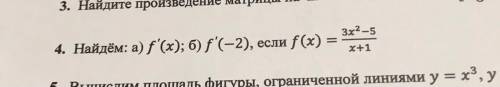
Решение.
По определению векторного произведения двух векторов модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. Поэтому для решения задачи найдем сначала векторное произведение , а потом его модуль. Согласно
имеем
а модуль
Искомая площадь параллелограмма
S = 19,26 кв. ед.
Замечание.
Векторное произведение можно было сразу определить по формуле
в которой следует взять
ax = 5; ay = -4; az = 7;
bx = 1; by = 1; bz = -2.
Фигура состоит из семи прямоугольников
№1 - "ножки человечка" - 2шт
№2 - "ручки человечка" - 2шт
№3 - "голова человечка" - 1шт
№4 - "шея человечка" - 1шт
№5 - "туловище человечка" - 1шт
Всего - 7 прямоугольников
А теперь решение:
1) 12 × 2 = 24 × 2 = 48 (площадь двух прямоугольников №1)
2) 8 × 2 = 16 × 2 = 32 (площадь двух прямоугольников №2)
3) 6 × 4 = 24 (площадь прямоугольника №3)
4) 2 × 2 = 4 (площадь прямоугольника №4)
5) 12 × 10 = 120 (площадь прямоугольника №5)
6) 48 + 32 + 24 + 4 + 120 = 228 (площадь фигуры)
ОТВЕТ: 228