
Обычные задачи на производительность.
1. Производительность первого: 1/15 в час
Второго: 1/х в час, вместе: 1/6 в час
1/15+1/х=1/6
2/30+1/х=5/30
1/х=3/30=1/10
х=10,
ответ: 1/10 в час, или он сделает всю работу за 10 часов
2. Матроскин: 1/11, Шарик: 1/9, вместе: 1/х
1/11+1/9=1/х
9/99+11/99=1/х
20/99=1/х
х=99/20=4.95,
ответ: они вместе сделают работу за 4.95 дней
3. По той же схеме, но одна труба работает в минус, т.к. сливает воду
1/7-1/8=1/х
8/56-7/56=1/х
1/56=1/х
х=56,
ответ: бассейн будет наполнен за 56 часов
Номер 1: ОДЗ - Область допустимых значений. Такие значения икс, при которых существуют левая и правая части неравенства
Под буквой А нам подходят все иксы, так как нет никаких ограничений
Под буквой Б наше ОДЗ примет вид (для первой дроби) x∈(-∞;-3)∪(-3;+∞), а для второй дроби ОДЗ x∈(-∞;3)∪(3;+∞), так как при x = ±3 у нас в знаменателях оказываются нули, чего быть недолжно
Под буквой В упростим знаменатель второй дроби, вынеся общий множитель. И будет тогда x(x+2). ОДЗ первой дроби x∈(-∞;-2)∪(-2;+∞), а второй дроби x∈(-∞;-2)∪(-2;0)∪(0;+∞), так как при x = -2 и x = 0 у нас нули в знаменателях
Номер 2: Запишем суммы:
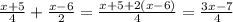
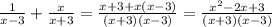
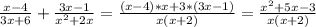
Номер 3: ОДЗ несократимых дробей: 1-ая дробь - все числа. 2-ая - все числа, кроме x = ±3. 3-я - все числа, кроме x=0 и x= -2
Номер 4:
Найдем значение дроби 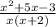 при x = -1. Тогда
при x = -1. Тогда 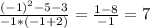
При х = 0.25 у нас будет 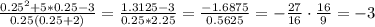
При х = 2 у нас будет 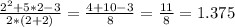
Пошаговое объяснение:
допустимые значения указываем по знаменателю.
для этого нужно понимать, что нельзя делить на 0
следовательно знаменатель не может быть равен 0
из этого получаем такие ответы:
1) а≠0
2)х+4,3≠0 отсюда х≠-4,3
3)5х≠0 отсюда х≠0
4)64-5х≠0 отсюда 5х≠64 и х≠12,8
5) (х+7)(х-10)≠0 отсюда х+7≠0, х≠-7 и х-10≠0, х≠10
можно лучший ответ?)