* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Дано:
а) ∠А1В1С1 - линейный угол двугранного угла АВВ1С,
т.к. данная фигура - куб.
б) Надо найти угол между плоскостями
∠ADB - линейный угол двугранного угла ADD1B;
в) Проведем B1K; проведем KE || AA1; проведем диагональ квадрата ВЕ. Требуется найти линейную меру двугранного угла между
плоскостями АА1В1В и KB1BE. А1В1 ⊥ ВВ1, B1K ⊥ ВВ1.
Таким образом, ∠А1В1K - линейный угол двугранного угла ABB1K.
Пошаговое объяснение:
Пусть в некоторый момент мы перевернули 4 стакана, из которых k стаканов стояли вверх дном, а 4 – k – правильно (k может принимать значения от 0 до 4). После переворачивания из этих четырёх стаканов k будут стоять правильно, а 4 – k – вверх дном. Таким образом, количество стаканов, стоящих вверх дном, изменится на чётное число 4 – k – k = 2(2 – k). Таким образом, чётность числа стаканов, стоящих вверх дном, не меняется. Поэтому в любой момент имеется нечётное число стаканов, стоящих вверх дном (так как вначале так стояли 7 стаканов).
Второй Заметим, что каждый стакан должен быть перевернут нечётное число раз, а всего стаканов нечётное число, то есть мы должны сделать нечётное число переворотов. Однако при каждом ходе переворачивается чётное число стаканов. Следовательно, перевернуть все стаканы вниз дном невозможно.
Минимум:
1. v=80 км/ч
Т=3ч
тогда S=V*T=80*3=240км
2. Т=3ч
S=180 км
тогда V= S:T=180:3=60 км/ч
3. S=600 км
V= 120 км/ч
T=S:V=600:120=5ч
Базовый: S Т
1. автомобиль 96км 2ч
велосипедист 72 км 6ч
1) Vа= 96:2=48 км/ч
2) Vв= 72:6=12 км/ч
3)
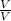= 48:12=4
ответ: в 4 раза
2. Всего S=723 км T=13ч
Т1= 9ч V1=55км/ч
1)S1= 55*9=495 км
2)Sост=723-495=228км
3)Тост=13-9=4 ч
4)V2=228:4=57 км/ч
ответ: 57 км/ч
Высокий:
S=56 км
Т=2ч
V1=12км/ч
1) S1= 12*2=24 км
2)S2=56-24=32 км
3) V2=32:2=16 км/ч
ответ: 16 км/ч