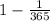 , далее возьмемь третього человека, вероятность того, что его день рождение не совпадеть из первыми двумя равна -
, далее возьмемь третього человека, вероятность того, что его день рождение не совпадеть из первыми двумя равна - 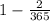 , идем по аналогии и находим вероятности для следующих человек в групе. Общая формула нахождение вероятности будет выглядеть так
, идем по аналогии и находим вероятности для следующих человек в групе. Общая формула нахождение вероятности будет выглядеть так 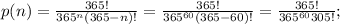
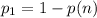 ; Тепер все посчитаем.
; Тепер все посчитаем.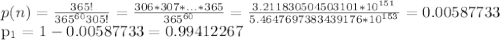
1480-1230=250 первое
1480-1010=470 второе
470+250=720
1480-720=760 третье