Математика: Вдвдыд Ьччдябчю Ададвббв влыды

Вдвдыд
Ьччдябчю
Ададвббв
влыды

👇

Увидеть ответ

Ответ:

sertarsertar205

05.08.2020

со го окопо

ошплелп

ьаллал

лалншнб

4,7(69 оценок)

Ответ:

Mazhor1

05.08.2020

ответ:ВАЯПВАЯПаа

ЯПВАРПЯПвпк

Пошаговое объяснение:пывпавепвпкева

ыяапняыуншды11.чрвк

4,6(27 оценок)

Открыть все ответы

Ответ:

AnyaManankina

05.08.2020

Задачу можно решить методом «научного тыка»

Допустим, в какой-то момент малыш Федя обгоняет Соню на ходулях. Отметим это место специальной меткой, как условное начало круга. Как только он обгоняет Соню, он понимает, что (теперь уже) она – впереди него на расстоянии длины круговой дорожки (фактически она почти впритык позади него, но ведь дорожка круговая (!), а значит, Соня, как бы и впереди на расстоянии длины дорожки).

Пускай теперь до нового места встречи Соня пройдёт от метки какую-то часть круговой дорожки, назовём это «кусок дорожки», а малыш Федя до этого нового места встречи проедет на велосипеде целый круг и ещё такую же часть дорожки, т.е. такой же «кусок», как и Соня.

Новое место встречи, таким образом, сместилось от начальной метки на «кусок дорожки».

После второй встречи, Федя опять обгонит Соню и потом опять встретится с ней уже в третий раз со смещением ещё на один «кусок дорожки» от предыдущего места встречи, которое и так уже было смещено от начальной метки на «кусок дорожки», стало быть, третья встреча сместится от начальной метки на «два куска дорожки».

Второе место встречи сместилось от начальной метки
на «кусок дорожки», а Федя проехал лишний круг.

Третье место встречи сместилось от начальной метки
на «два куска дорожки», а Федя проехал два лишних круга.

Четвёртое место встречи сместится от начальной метки
на «три куска дорожки», а Федя проедет три лишних круга.

Пятое место встречи сместится от начальной метки
на «четыре куска дорожки», а Федя проедет четыре лишних круга.

Заметим, что если бы Соня к пятому месту встречи, смещённому от начальной метки на «четыре куска дорожки бы целый круг, то тогда Федя проехал бы 4 лишних круга и ещё «четыре куска дорожки», т.е. такое же расстояние, как и Соня, а значит ещё один добавочный круг.

И в таком случае, получилось бы, что Соня один круг, а Федя проехал пять кругов, что как раз и сходится с их соотношением скорости. Всё правильно, Федя ведь ездит в 5 раз быстрее, а значит, он и должен проехать в 5 раз больше, чем проходит Соня!

Значит, наше предположение верно. К пятой встрече Соня проходит полный круг, а стало быть, она приходит к начальной метке, которую мы отметили в месте первой встречи, т.е. место пятой встречи совпадает с местом первой встречи. Дальнейшие встречи станут совпадать со встречами в первом цикле рассуждений. Таким образом, всего существует 4 разных места, где Федя обгоняет Соню.

Так же, эту задачу можно решить и «аналитически», через введение неизвестного параметра скорости, и рассмотрения относительной скорости участников, т.е. скорости сближения.

Пусть скорость Сони равна v .

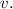Тогда скорость Феди равна 5v .

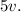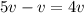Когда Федя догоняет Соню, их скорость сближения равна 5v - v = 4v

(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения. Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.

О т в е т : (Б) в 4 точках.

4,6(63 оценок)

Ответ:

эмилисенок2

05.08.2020

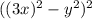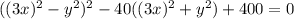Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: $((3x)^{2}-y^{2})^{2}$ ; В следующих двух слагаемых вынесем общий множитель "40": $40(9x^{2}+y^{2})=40((3x)^{2}+y^{2})$ ; В итоге получим следующее уравнение: $((3x)^{2}-y^{2})^{2}-40((3x)^{2}+y^{2})+400=0$ . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. 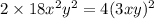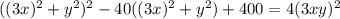Пусть в первой скобке вместо $(3x)^{2}-y^{2}$ будет стоять $(3x)^{2}+y^{2}$ ; Это приведет к тому, что придется убавить $2\times 18x^2y^2=4(3xy)^{2}$ ; В итоге: $((3x)^{2}+y^{2})^{2}-40((3x)^{2}+y^{2})+400= 4(3xy)^{2}$ ; Слева стоит квадрат суммы. 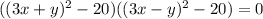Уравнение примет вид: $((3x)^{2}+y^{2}-20)^{2}=(6xy)^{2} \Leftrightarrow ((3x)^{2}+y^{2}-20+6xy)((3x)^{2}+y^{2}-20-6xy)=0$ ; Сворачивая еще раз: $((3x+y)^{2}-20)((3x-y)^{2}-20)=0$ ; Получаем серию прямых: $\pm 3x+\sqrt{20},\; \pm3x-\sqrt{20}$ ; А теперь приступим к рассмотрению первого уравнения.

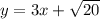Это уравнение задает круг с центром в точке (0, 0) и радиусом $\sqrt{2}$ ; Рассмотрим прямую $y=3x+\sqrt{20}$ ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 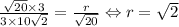$\frac{\sqrt{20}\times 3}{3\times 10\sqrt{2}}=\frac{r}{\sqrt{20}} \Leftrightarrow r=\sqrt{2}$ ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 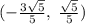$(-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5} } )$ ; Ну а все решения:

$(\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5})$