пришлось удалить т к. ответили(o´･_･)っ
* Какому числу равна сумма ABCD+BADC+CDBA+DCAB, если А+В+С+D=21?
ABCD+BADC+CDBA+DCAB = 1000(A+B+C+D)+100(A+B+C+D)+10(A+B+C+D)+(A+B+C+D)=1111(A+B+C+D)=1111*21=23331
ответ: 23331
**Найти сумму ABCD+BCDA+CABC+DDAB, если А+В+С+D=33?
ABCD+BCDA+CABC+DDAB = 1000(A+B+C+D)+100(B+C+A+D)+10(C+D+B+A)+(D+A+C+B)=1111(A+B+C+D)=1111*33=36663
ответ: 36663
*** Найти сумму A+B+C+D, если CABC+DDAB+BCDA+ABCD=39996.
ABCD+BСDА+CABC+DDAB = 1000(C+D+B+A)+100(A+D+C+B)+10(B+A+D+C)+(C+B+A+D)=1111(A+B+C+D)
1111(A+B+C+D)=39996
A+B+C+D=39996:1111
A+B+C+D=36
ответ: 36
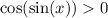
Косинус больше нуля при таких значениях его аргумента:
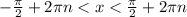
В нашем случае его аргумент – синус, значит:
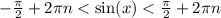
Синус существует в пределах от -1 до 1 включая концы. Переберём несколько значений n:
1. n = 0
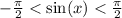
Имеем ввиду, что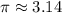 
, а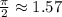 
. Поэтому для n = 0 неравенство выполняется для всех х;
2. n = -1:
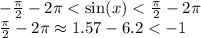
Так как верхняя граница меньше -1, то нижняя и подавно, следовательно неравенство не выполняется.
3. n = 1:
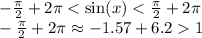
В этом случае нижняя граница больше 1, а синус нестрого меньше 1, значит неравенство опять же не выполняется.
В итоге получили единственный случай при котором выполняется неравенство – при n = 0.
ответ: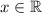 
.
arccos 1/2 + arcctg 1
п/3 + п/4
7п/12 (105°)