400
Пошаговое объяснение:
Решил Мудrost
Пусть х- это задуманное число.
Раз половина задуманного числа на 120 больше одной пятой задуманного числа,то одна пятая числа на 120 меньше чем половина задуманного числа, значит чтобы получилось равенство между (1/2)х и (1/5)х, нужно к (1/5)х прибавить 120, а (1/2)х оставить.У нас получается равенство(уравнение).
Составим и решим уравнение:
(1/2)х=120+(1/5)х
(1/2)х оставляем, а (1/5)х переносим влево поменяв знак на противоположный(-):
(1/2)х-(1/5)х=120
Приводим дроби (1/2)х и (1/5)х к общему знаменателю (10):
Получаем:
(5/10)х-(2/10)х=120
Раз дроби с одинаковым знаменателем, то их можно вычитать и складывать, в нашем случае их нужно вычесть:
(3/10)х=120
Теперь, чтобы избавиться от (3/10) в левой части уравнения, нужно обе части уравнения поделить на эту дробь:
х=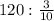
Меняем местами числитель (3) и знаменатель (10) у дроби 3/10 и число 120 делаем неправильной дробью 120/1 (Пояснение: единицу я не написал, потому что это не очень важно, она все равно в вычислениях не имеет значения) :
х=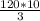
х=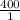
х=400
Пояснения знаков:
*-знак умножения
/-дробная черта
Ещё кое-что важное, я некоторые дроби с х(иксом, то есть неизвестным числом) взял в скобки чтобы показать что х(икс) находится не в знаменателе, а умножается на эту дробь.
Решил Мудrost
Обозначим α - угол между диагоналями АС и BD,
по свойствам параллелограмма
∠NKL=∠NML=α.
Пусть КL=4x, LM=5x, тогда KL : LM = 4 : 5;
АС=2у, BD=3y, тогда AС: BD= 2 : 3.
Δ CML подобен Δ CBD ( LM ║ BD).
Из подобия
СL : CB = LM : BD = 5x : 3y ⇒ (СB-LB) : CB= 5x : 3y⇒ LB : CB=1-(5x/3y)
Δ BKL подобен Δ АВС ( KL ║ AC).
Из подобия
BK: BA= КL : AC = 4x : 2у = 2х : у
и
BK: BA= BL: BC
2x/y=1-(5x/3y)
x : y=3:11.
S( KLMN) : S ( ABCD)=(KL·LM·sinα) : (AC·BD·sinα/2)=
=(4x·5x·sinα) : (2y·3y·sinα/2)=20x² : 3y²=(10/3)·(x/y)²=(20/3)·9/121=60/121
О т в е т. 60 : 121.