Ено́ты — род хищных млекопитающих семейства енотовых. Представители рода — обитатели Америки. . Включает семь видов. Туловище и конечности енотов короткие, голова широкая, мордочка заостренная. Уши большие, округлые. Еноты отличаются густым и длинным мехом.
На территории Евразии и, в частности, в России емеется один вид-енот-плоскун Он распространен в лесах Центральной и Северной Америки, акклиматизирован в Германии, Белоруссии, Азербайджане, на Дальнем Востоке. В Центральной Америке и на севере Южной Америки водится близкий к полоскуну вид — енот-ракоед, отличающийся удлиненным телом, гладким коротким мехом, непушистым хвостом. По образу жизни и питания он сходен с полоскуном.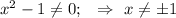

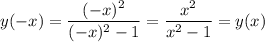
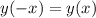 , то эта функция четная.
, то эта функция четная.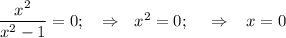
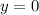
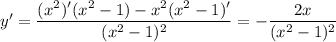
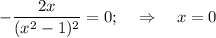
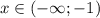 и
и 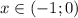 , а убывает на промежутке
, а убывает на промежутке 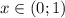 и
и 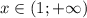
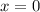 производная функции меняет знак с (+) на (-), следовательно, точка
производная функции меняет знак с (+) на (-), следовательно, точка 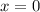 - точка максимума.
- точка максимума.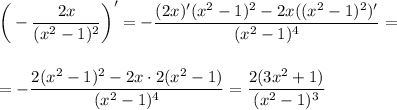
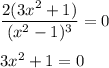
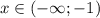 и
и 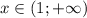 функция вогнута, а на промежутке
функция вогнута, а на промежутке 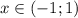 функция выпукла.
функция выпукла.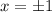
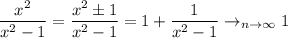
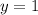 - горизонтальная асимтота
- горизонтальная асимтота