
(2; 0,5)
Пошаговое объяснение:
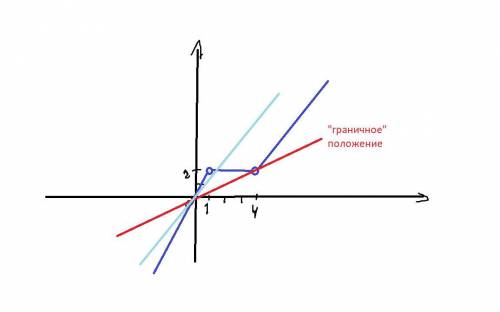
Очевидно, К=2 нам не подходит, т.к. такая прямая (F(x) = kx - линейная функция, график прямая) будет совпадать с 2х.
Рассмотрим график; чтобы было три пересечения, прямая должна пересекать все три "куска" графика.
Первую часть, у=2х, пересекает при К!=2.Вторую часть, у=2, пересекает при всех К принадлежащих интервалу (2;0.5) - 0.5 получаем из уравнения 2=4К (берем "граничное" положение (при котором УЖЕ нельзя найти три пересечения) F(x)=kx и подставляем.Третью часть пересекает при соблюдении первого условия, т.к. если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую.Имеем К!=2 и 2<K<0,5 => К принадлежит (2; 0,5).
∠BCA = 70°; ∠CBA = 55°; ∠BAC = 55°
Пошаговое объяснение:
Дано:
Треугольник ABC; ∠BCE = 130°
Найти:
∠CAB; ∠CBA; ∠ACB
1) ∠ACB и ∠BCA - смежные, след. их сумма 180°, следовательно ∠ACB = 180° - ∠BCA = 70°
2) ∠CBA = ∠BAC (по свойству равноб. треугольника).
Сумма углов треугольника = 180°, след. ∠CBA и ∠BAC = (180° - 70°) : 2 = 55°
ответ: ∠BCA = 70°; ∠CBA = 55°; ∠BAC = 55°