Пошаговое объяснение:
1. По условию задачи в урне находятся 12 белых и 8 черных шаров.
Вычислим общее количество шаров.
12 + 8 = 20.
2. Вероятность события равна частному от деления числа благоприятных исходов на общее количество исходов.
Вытащили шар.
Тогда вероятность того, что он черный P1 = 8/20 = 2/5.
Вероятность того, что он белый P2 = 12/20 = 3/5.
3. Вытащили 2 шара.
Если первый шар белый, то вероятность того, что второй черный P3 = 8 / (20 - 1) = 8/19.
Если первый шар черный, то вероятность того, что второй белый P4 = 12/ (20 - 1) = 12/19.
4. Найдем вероятность того, шары разного цвета.
P = 3/5 * 8/19 + 2/5 * 12/19 = 48/95.
ответ: вероятность того, что шар черный - 2/5, белый - 3/5, 2 шара разного цвета 48/95.
Для нахождения угла по его синусу, косинусу и т. д. используются так называемые аркфункции: арксинус, арккосинус и т. д. Их обозначают arcsin a, arccos a и т. д.
На Вашем калькуляторе над кнопками с синусом и косинусом есть надписи: sin в степени -1 и cos в степени -1.Это создатели калькулятора так кратко обозначили аркфункции. Чтобы ими воспользоваться, надо набрать число ( например, 0,4965), нажать клавишу SHIFT или 2nd, а затем клавишу, над которой написано cos в степени -1 и равно. У Вас получится угол, косинус которого равен 0,4965.
ошаговое объяснение:
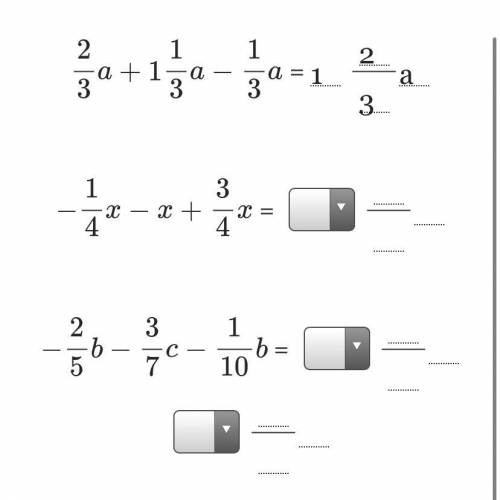
1)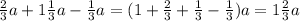
ответ: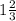
2)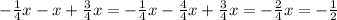
ответ: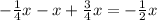
3)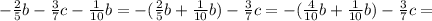
ответ: