Пошаговое объяснение:
1) для нахождения экстремума сперва найдем критические точки.
для этого найдем первую производную
![y=\frac{x^2-2x+2}{x-1} =\left[\begin{array}{ccc}(\frac{u}{v} )'=\frac{u'v-uv'}{v^2} \\\\\end{array}\right] \\y' = \frac{x(x-2)}{(x-1)^2}](/tpl/images/1497/0391/47196.png)
теперь приравняем ее к 0
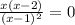⇒ х₁ = 0; х₂ = 2; это точки экстремума
теперь найдем значения функции в этих точках
y(0) = -2
y(2) = 2
таким образом мы нашли экстремумы функции
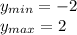
2) вся теория та же, запишу только вычисления
y=x-ln(1+x)
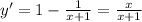
здесь будет одна точка экстремума
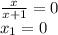
значение функции в этой точке
у(0)=0
теперь надо понять максимум это или минимум
для этого найдем вторую производную и ее значение в т х₁=0
если у"(х₁) будет >0 - значит точка x₁ = 0 точка минимума функции.
если у"(х₁) будет <0 - значит точка x₁ = 0 точка максимума функции.
итак, вторая производная
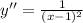
y''(0)=1 > 0 - значит точка x₁ = 0 точка минимума функции.
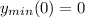
Для того, чтобы сравнить дроби приведём их все к общему знаменателю, если дробь смешанная, то переведём её в неправильную, общий знаменатель для всех дробей равен 30 (для его нахождения мы нашли НОК "всех" знаменателей. Тогда получим:
\begin{gathered}\displaystyle 1)\quad \frac{5}{6} =\frac{25}{30} 2)\quad \frac{1}{3} =\frac{10}{30} 3)\quad \frac{3}{5} =\frac{18}{30} 4)\quad \frac{5}{3} =\frac{50}{30} 5)\quad 1 \frac{1}{6} =\frac{7}{6}=\frac{35}{30} 6)\quad 2\frac{2}{3} =\frac{8}{3}=\frac{80}{30} end{gathered}
1)
6
5
=
30
25
2)
3
1
=
30
10
3)
5
3
=
30
18
4)
3
5
=
30
50
5)1
6
1
=
6
7
=
30
35
6)2
3
2
=
3
8
=
30
80
5
3
=
30
18
4)
3
5
=
30
50
5)1
6
1
=
6
7
=
30
35
6)2
3
2
=
3
8
=
30
80
Теперь сравнивать числа стало гораздо проще. Просто сравним числители и получим, что:
80 > 50 > 35 > 25 > 18 > 1080>50>35>25>18>10
6) > 4) > 5) > 1) > 3) > 2)6)>4)>5)>1)>3)>2)
Подставим вместо номеров изначальныеПодставим вместо номеров изначальные дроби:
\displaystyle 2 \frac{2}{3} ;\quad \frac{5}{3} ;\quad 1\frac{1}{6} ;\quad \frac{5}{6} ;\quad \frac{3}{5} ;\quad \frac{1}{3}дроби:
\displaystyle 2 \frac{2}{3} ;\quad \frac{5}{3} ;\quad 1\frac{1}{6} ;\quad \frac{5}{6} ;\quad \frac{3}{5} ;\quad \frac{1}{3}2
3
2
;
3
5
;1
6
1
;
6
5
;
5
3
;
3
1
(5- x) ²+10x
25-10х+х²+10х
25+х²
При х=5:
25+5²=50