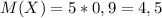, то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
Пошаговое объяснение:
Пусть проводится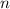 
независимых испытаний, даже не обязательно повторных. И в каждом из которых случайное событие 
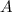может появиться с вероятностью 
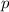. Тогда случайная величина 
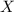, это число появлений события 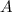в данной серии испытаний, имеет биномиальное распределение.
Кондрат последовательно заходит в 5 автобусов, то есть совершается серия и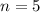 
и только 5 похождений в различные автобусы, где вероятность встретить контролера в каждом из них составляет 
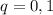. Тогда вероятность НЕ встретить контролера в автобусе равна 
.
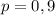Математическое ожидание при биномиальном распределении рассчитывается согласно формуле:
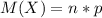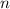, где - количество независимых испытаний, то есть количество автобусов, в которое последовательно заходит Кондрат, 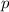- вероятность появления события 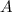, то есть автобуса без контролера.
Найдем математическое ожидание числа автобусов в которые успеет зайти Кондрат:
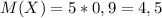- то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
ответ на задачу: 150.000 рублей; сумма всех натуральных чисел от 1 до 33 равна 561.
Пошаговое объяснение:
Первая задача решается методом пропорции, то есть:
если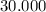
рублей это 20% от всей суммы кредита
Тогда
рублей это 100% всей суммы кредита.
Получаем, что вся сумма кредита равна:
Второе задание решается, если вспомнить, что сумма чисел от 1 до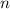
(где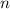 
- наибольшее среди всего ряда натуральных чисел начиная с 1), вычисляется по формуле арифметической прогрессии с шагом 1:
Где
. Подставив данное значение найдем сумму натуральных чисел от 1 до 33:
Проверить это можно, посчитав вручную:
В данном случае я считал сначала сумму от 1 до 10, следом сумму от 11 до 20, далее от 21 до 30 и от 31 до 33. Получили аналогичный ответ.