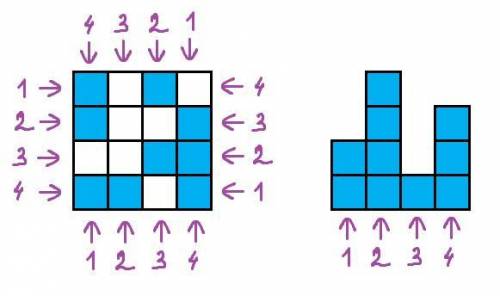
На конструкцию можно смотреть с 4 сторон: спереди, слева, сзади и справа. Просчитаем максимально возможное число кубиков в каждом случае, зная что максимальные количества кубиков в башнях по линиям соответственно равны 2, 4, 1, 3.
1. Смотрим спереди: соответствующие линии показаны на картинке. Максимальные количества башен по линиям соответственно равны 3, 1, 2, 3.
Итого: 2·3+4·1+1·2+3·3=6+4+2+9=21
2. Смотрим слева. Максимальные количества башен по линиям соответственно равны 2, 2, 2, 3.
Итого: 2·2+4·2+1·2+3·3=4+8+2+9=23
3. Смотрим сзади. Максимальные количества башен по линиям соответственно равны 3, 2, 1, 3.
Итого: 2·3+4·2+1·1+3·3=6+8+1+9=24
4. Смотрим справа. Максимальные количества башен по линиям соответственно равны 3, 2, 2, 2.
Итого: 2·3+4·2+1·2+3·2=6+8+2+6=22
Максимальное количество при взгляде сзади - 24.
ответ: 24
ответ:
пошаговое объяснение:
150 100 – 697 · 208 + 182 620 : 397 = 5 584
697 · 208=144 976
182 620 : 397=460
150 100-144 976=5 124
5 124+460=5 584
( 41 · 134 + 11 978 ) : ( 1 211 – 899 ) = 56
41 · 134=5 494
5 494+11 978 =17 472
1 211 – 899 =312
17 472: 312=56
271 100 – 790 · 306 + 5 711 540 : 809 = 36 420
790 · 306=241 740
5 711 540 : 809 =7 060
271 100-241 740=29 360
29 360+7 060=36 420
7 091 + 19 663 – ( 243 916 + 75 446 ) : 527 · 37 = 4 332
243 916 + 75 446=319 362
319 362 : 527=606
606 · 37=22 422
7 091 + 19 663=26 754
26 754-22 422=4 332
700 200 – 615 880 : 346 · 307 + 46 260 = 200 000
615 880 : 346= 1 780
1 780· 307=546 460
700 200 – 546 460=153 740
153 740+ 46 260 = 200 000
178 · 406 + 37 832 – 558 182 : 397 = 108 694
178 · 406=72 268
558 182 : 397=1 406
72 268 + 37 832=110 100
110 100-1 406=108 694
369 · 304 + 961 620 : ( 1 357 – 840 ) =114 036
( 1 357 – 840) =517
369 · 304 =112 176
961 620 : 517=1 860
112 176+1 860=114 036