разложим на простые делители
74=2*37
значит их сумма будет равна 37+2=39
Пошаговое объяснение: «ВАЛЛ-И» (обратная аббревиатура с англ. — «Вселенский Аннигилятор Ландшафтный Лёгкий, Интеллектуальный»[5]; англ. WALL-E, [ˈwɔːli], обратная аббревиатура Waste Allocation Load Lifter, Earth-class[1] — дословно: мусоропогрузчик земного класса) — полнометражный компьютерный анимационный научно-фантастический фильм 2008 года, созданный Pixar Animation Studios. Премьера фильма в США состоялась 27 июня 2008 года, а премьера в России — 3 июля 2008 года. На DVD и Blu-ray фильм был выпущен 18 ноября 2008 года[6]. Режиссёром фильма выступил Эндрю Стэнтон, чей предыдущий фильм «В поисках Немо» получил «Оскара» за лучший анимационный полнометражный фильм. Джим Моррис, ранее работавший в компании Lucasfilm, стал продюсером картины.
Удачи!
Если правильно сделай ответ лучшим
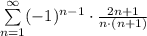
Исследуем этот ряд на абсолютную сходимость.
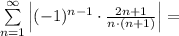
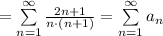
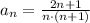
Рассмотрим ряд
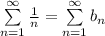
Используем предельный признак сравнения:
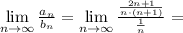
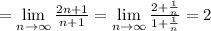
Значит ряды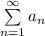 
и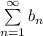 
сходятся или расходятся одновременно, но ряд
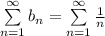
это гармонический ряд, который расходится. Значит и ряд
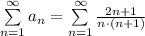
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
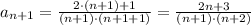
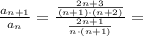
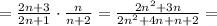
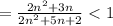
т.к.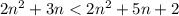 
⇔ 
⇔ 
.
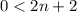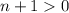То есть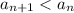 
.
То есть последовательность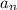 
монотонно убвывает.
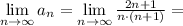
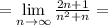
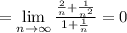
То есть последовательность 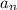монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
Наименьший простой делитель числа 74 равен 2.
Наибольший простой делитель числа 74 равен 37.
Их сумма: 2 + 37 = 39
ответ: 39