7,5
Пошаговое объяснение:
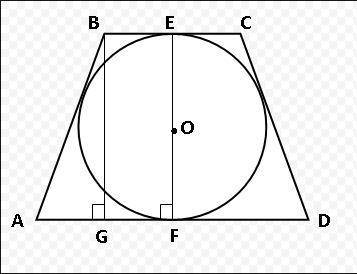
Пусть основание ВС=3, значит BE=1,5=EC.
Отрезки касательных из точки В равны, значит часть стороны АВ равно 1,5 а остальное пусть равно x. Опустим высоту BG = 6 (как два радиуса).
И если опустить из точки С высоту, то основание АD будет разбито на отрезки 3 и два равных по бокам, пусть они будут равны y.
Можно составить уравнения:
1. Если в четырехугольник можно вписать окружность, то сумма противоположных сторон равны:
1,5+x+1,5+x(сумма боковых сторон)=3+3+y+y (сумма оснований)
3+2x=6+2y
x=1,5+y
2. Так же треугольник ABG прямоугольный, можно составить уравнение согласно теореме Пифагора:
(1,5+x)²=36+y²
Можно решать через систему данных уравнений, подставляем значение x:
(1,5+1,5+y)²=36+y²
(3+y)²=36+y²
9+6y+y²=36=y²
y=
x=6
Значит боковая сторона равна: 6+1,5=7,5
1) 20 = 2² · 5; 12 = 2² · 3; НОК = 2² · 3 · 5 = 60 - общ. знаменатель
60 : 20 = 3 - доп. множ. к 7/20 = (7·3)/(20·3) = 21/60
60 : 12 = 5 - доп. множ. к 5/12 = (5·5)/(12·5) = 25/60
ответ: 7/20 и 5/12 = 21/60 и 25/60.
3) 16 = 2⁴; 12 = 2² · 3; НОК = 2⁴ · 3 = 48 - общ. знаменатель
48 : 16 = 3 - доп. множ. к 3/16 = (3·3)/(16·3) = 9/48
48 : 12 = 4 - доп. множ. к 7/12 = (7·4)/(12·4) = 28/48
ответ: 3/16 и 7/12 = 9/48 и 28/48.
5) 12 = 2² · 3; 9 = 3²; НОК = 2² · 3² = 36 - общ. знаменатель
36 : 12 = 3 - доп. множ. к 1/12 = (1·3)/(12·3) = 3/36
36 : 9 = 4 - доп. множ. к 2/9 = (2·4)/(9·4) = 8/36
ответ: 1/12 и 2/9 = 3/36 и 8/36.
7) 15 = 3 · 5; 12 = 2² · 3; НОК = 2² · 3 · 5 = 60 - общ. знаменатель
60 : 15 = 4 - доп. множ. к 8/15 = (8·4)/(15·4) = 32/60
60 : 12 = 5 - доп. множ. к 5/12 = (5·5)/(12·5) = 25/60
ответ: 8/15 и 5/12 = 32/60 и 25/60.