Пошаговое объяснение:
1) Докажем существование прямой.
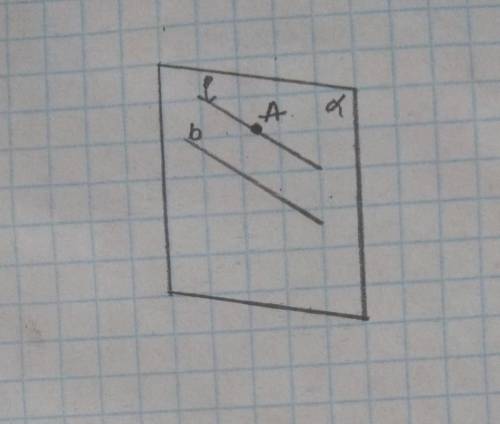
Пусть дана прямая b и точка А, не лежащая на этой прямой. Тогда через них проходит единственная плоскость a(см. рисунок). В этой плоскости, как известно из планиметрии, существует прямая l, проходящая через точку А и параллельная прямой b.
2. Докажем единственность прямой.
Предположим, что существует ещё одна прямая l1, проходящая через точку А и параллельная прямой b. Тогда прямая l1 должна лежать в одной плоскости с точкой А и прямой b, тоесть в плоскости а. Из курса планиметрии известно, что в плоскости а через точку А проходит единственная прямая, параллельная прямой b. Значит, прямая l1 совпадает с прямой l.
Теорема доказана
1) две целых 3 восьмых - 1 целая одна шестая м должны убрать целые числа, получается, 19 восьмых - 7 шестых, теперь приводим к общему знаменателю, получаем 57 двадцать четвёртых - 28 двадцать четрёртых = 29 двадцать четвёртых.
2) опять переводим целые в дробь и получаем: 29 двадцать четвёртых : 29 двенадцатых. приводим к общему знаменателю, получается 29 двадцать четвёртых : 58 двадцать четвёртых. теперь чтобы решить, надо перевернуть вторую дробь. получаем: 29 двадцать четвёртых умножить на 24 пятьдесят восьмых, 24 сокращаем, получается дробь 29 пятьдесят восьмых.
второй пример попробуй по той же технологии, ну чтобы сама поняла. а если не получится, пиши в личку)
СК - биссектриса, так как делит угол пополам