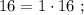
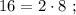
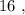т.е.: 
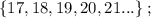
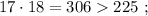
каждое – будет, очевидно, больше чем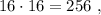 
т.е. больше 
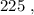а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.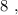
т.е.: 
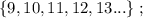
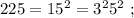
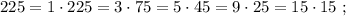
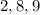и 
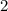и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы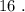 
и никаких натуральных чисел нет. и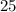 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы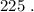 
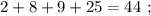
Получится равнобедренный треугольник с углами у основания по 45 градусов и равными боковыми сторонами по 8 см.
Так как два угла треугольника-сечения известны (по 45), то можно посчитать оставшийся угол = 180 - 45 - 45 = 90. Следовательно, треугольник прямоугольный.
Диаметр (или 2 радиуса) основания конуса будет равен основанию прямоугольника (то есть неизвестной пока стороне. По совместительству, эта сторона будет являться гипотенузой.
По теореме Пифагора, гипотенуза равна корню квадратному из суммы квадратов катетов. То есть
Мы нашли гипотенузу сечения, а следовательно и диаметр конуса.
Диаметр = 2 радиусам. Т.е. радиус =
Формула объёма конуса:
Осталось найти высоту.
Из вершины треугольника-сечения опустим высоту. Она попадёт прямо на середину его основания, т.е. поделит его пополам. Эта высота образует прямоугольный треугольник, где высота и радиус конуса будут катетами, а образующая конуса - гипотенузой.
Найдём по теореме Пифагора высоту:
Подставляем в формулу объёма конуса всё найденное:
Если у вас