Пошаговое объяснение:
Начальная цена 100%
После увеличения на 50% цена стала 150% от начальной
Нужно, чтобы цена составляла 120% от начальной после скидки, но тут подвох.
скидывать мы будем цену от текущей, которая составляет 150% от начальной. Простое решение типа 150-120 тут будет неверным.
Нам надо скинуть 30% от начальной цены, но для текущей(которая 150% начальной) это будет равно:
30/150*100 = 20% ОТ ТЕКУЩЕЙ.
либо, если в такой записи будет проще:
(1-120/150)*100% = 20%
Т.е. как ответ:
Нужно скинуть 20% от текущей июньской цены, чтобы получить цену в конце сезона на 20% выше январской
ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
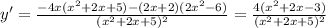
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
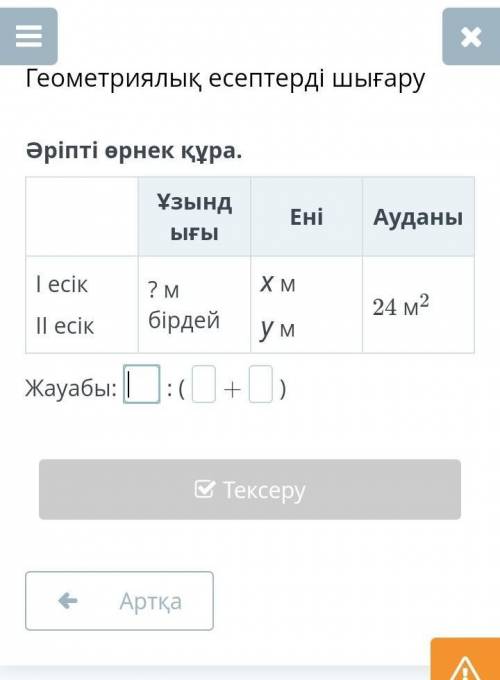
24м2:(х+у) дұрыс болса рахмет