
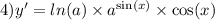
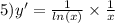
ответ:ответ. 102. Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
Пошаговое объяснение:
11х-х²<0
х*(11-х)<0
1. Приравниваем к нулю левую часть. 11х-х²=0; х*(11-х)=0
Получаем два корня х=0 и х=11
2. Разбиваем числовую ось на промежутки (-∞;0);(0;11);(11;+∞)
3. Берем произвольные значения из каждого промежутка, чтобы установить знак левой части неравенства.
В первом промежутке, например, возьмем х= -2, получаем
11*(-2)-(-2)²=-22-4=-26 получили знак минус
Для второго промежутка взяли х=1, получили 11-1=10 плюс
ДЛя третьего взяли х= 12, получили 11*12-12²=132-144=-8 получили знак минус.
Собрали минусы и записали ответ.
х∈(-∞;0)∪(11;+∞)