раскроем модуль:
1) если cos x ≥ 0, то исходное уравнение примет вид 1 + 2sin x · cos x = 0.
воспользуемся формулой синуса двойного угла, получим:
1 + sin 2x = 0; sin 2x = -1;
2x = -π/2 + 2πn, n € z;
x = -π/4 + πn, n € z. так как cos x ≥ 0, то x = -π/4 + 2πk, k € z.
2) если cos x < 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. по формуле синуса двойного угла, имеем:
1 – sin 2x = 0; sin 2x = 1;
2x = π/2 + 2πn, n € z;
x = π/4 + πn, n € z. так как cos x < 0, то x = 5π/4 + 2πk, k € z.
3) наибольший отрицательный корень уравнения: -π/4; наименьший положительный корень уравнения: 5π/4.
искомая разность: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 · 180°/2 = 270°.
ответ: 270°. в)ты график функции y=tg(x) знаешь?
так вот для первого случая та часть что внизу оси х была отобразится зеркально вверх (для отрицательных х) ; верхняя часть останется без изменений.
а для второго случая, нижних частей тоже не будет, но каждая верхняя ветвь отобразится зеркально (налево) относительно оси y (для отрицательных значений х) , а для положительных х опять имеем верхнюю ветвь обычного графика tg(x)
кажется так должно получиться..
еcos x=1 cos x=-1
x=2pi*n
x=pi+2pi*n
=+-pi*n
ctg x=1 ctg x=-1
x=pi/4+pi*k
x=3pi/4+pi*k
используй свойство модулясли я правильно объяснил.. в голове-то у меня всё правильно нарисовалось, но вам туда г)
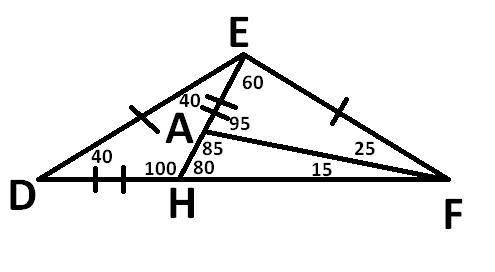
95°
Пошаговое объяснение:
Этот треугольник тупоугольный т.к. ∠DEF=180-40-40=100°;
Мы имеем ∠DFA=15; ∠DEA=40;
Далее эту задачу можно решить двумя :
Первый (Более простой) - ∠AFE=40-∠DFA=40-15=25°; ∠AEF=100-∠DEA=100-40=60°; ∠EAF=180-60-25=95°
Второй (Сложнее, но красивее) - Продолжим прямую EA до соприкосновения с прямой DF в точке H; ∠D=∠DEA=40°; ∠DHE=180-40-40=100°; ∠AHF=180-100=80°; ∠HAF=180-80-∠DFA=180-80-15=85°; ∠EAF=180-85=95°
Кстати, нету смысла писать одно и то же задание несколько раз, от этого всё равно нету толка - тебе в основном только я и отвечаю. Это лишь пустая трата для тебя.
12.3
Пошаговое объяснение:
размах ряда 18-5=13