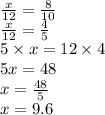
=-:мать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxa
:мать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxa
:мать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxa
:мать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxaмать шлюxa
Пошаговое объяснение:
х:12=8:10
x/12 = 4/5
5*x=12*4
5x=48
x=48/5
x=9.6