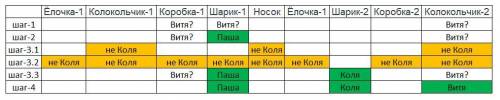
Рассмотрим условия.
1. "Витина игрушка висит третьей от ёлочки". Отсчитав третьи игрушки от елочки, получим, что Витина игрушка - либо первая коробка, либо первый шарик, либо второй колокольчик.
2. "Пашина между носком и коробкой". Между носком и коробкой висит первый шарик. Значит это игрушка Паши и она не может быть игрушкой Вити.
3.1. "Колина игрушка - это НЕ носок и НЕ колокольчик".
3.2. "Висит она НЕ рядом с носком и НЕ рядом с колокольчиком".
3.3. Единственная возможная игрушка Коли - второй шарик.
4. "Игрушки Вити, Паши и Коли НЕ висят рядом друг с другом". Поскольку первая коробка висит рядом с игрушкой Паши, то игрушка Вити - второй колокольчик.
ответ: колокольчик
Пошаговое объяснение:
1) (6y-1)(y+2)<(3y+4)(2y+1)
6y^2 +12y-y-2<6y^ +3y+8y+4
6y^2 -6y^2 +11y-11y<4+2
0<6
y принадлежит (-∞; +∞).
2) 4(х+2)<(х+3)^2 -2х
4x+8<x^2 +6x+9-2x
x^2 +4x+9-4x-8>0
x^2 +1>0
x^2>-1 - данное неравенство верно при любом значении x.
Следовательно, x принадлежит (-∞; +∞).
1) (3y-1)(2y+1)>(2y-1)(2+3y)
6y^2 +3y-2y-1>4y+6y^2 -2-3y
6y^2 -6y^2 +y-y>1-2
0>-1
x принадлежит (-∞; +∞).
2) (x-5)^2 +3x>7(1-x)
x^2 -10x+25+3x-7+7x>0
x^2 +18>0
x^2>-18 - данное неравенство верно при любом значении x.
Следовательно, x принадлежит (-∞; +∞).