 =
= 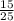
Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
1. Нули функции : y=x^2-4x-32 = 0.
Д = 16 + 4*32 = 144. х1 = (4 + 12)/2 = 8, х2 = (4 - 12)/2 = -4.
2. Точки пересечения графиков функций: y=(5x-6)^2 и y=(5x-7)^2 .
Раскроем скобки и приравняем функции:
25х² - 60х + 36 = 25х² - 70х + 49.
10х = 13,
х = 13/10, у = 1/4. Одна точка пересечения ((13/10); (1/4)).
3. Координаты точек пересечения параболы : y=x^2-7 и прямой y-x=5.
Приравняем: x^2-7 = x+5, x^2-x-12 = 0, Д = 1 + 4*12 = 49.
х1 = (1 + 7)/2 = 4, х2 = (1 - 7)/2 = -3.
Две точки пересечения: (4; 9) и ((-3; 2).