3)все 4 функции вида y = kx + b. если b > 0, то прямая соприкасается с осью ординат выше оси абсцисс, а если b < 0, то прямая соприкасается с осью ординат ниже оси абсцисс. значит, графики a и b соответствуют уравнениям 2 и 3, а графики c и d соответствуют уравнениям 1 и 4. определим теперь конкретно какой график к какому уравнению подходит. рассмотрим уравнение, в котором k = 2 y = 2x + 5, причём x = = 2,5. значит, прямая проходит через точку абсцисс 2,5. рассмотрим уравнение, в котором k = 1 y = x - 5, из свойств числового коэффициента b следует, что график проходит через точку ординат -5, а из формулы y = a(x - m)² следует, что точка соприкосновения оси абсцисс и прямой смещена вправо на 5. проведя аналогичные рассуждения с остальными двумя уравнениями и их графиками, придём к выводу, что1) - c2) - a3) - b4) – d
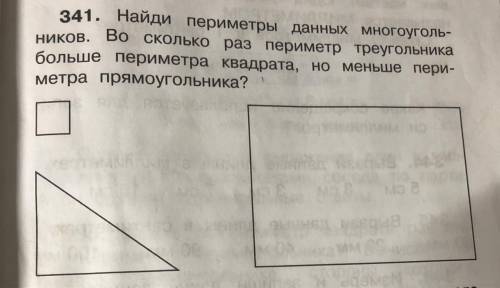
(Измерь линейкой их стороны)
(Допустим у квадрата ширина и длина - у)
Р=у•4=а (допустим периметр а)
(Допустим у треугольника 1 стор.- u 2 стор.-i 3 стор.- s)
Р=u+i+s=h (допустим периметр h)
(Допустим у прямоугольника ширина - х а длина -t)
Р=(х+t)•2=r (допустим периметр r)
1) H-a=V
2) R-h=p
(Пришлось делать в виде цифр ведь автор не написал их стороны)