1) 
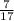-при выборе первого изделия (первое событие)
2) 
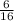- при выборе второго изделия (второе событие)
3) × = 
= 
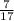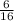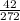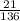
ответ. Вероятность равна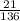
Пошаговое объяснение:
1) когда всего 17 изделий и 7 некачественных, находим вероятность, при которой нам попадается брак.
2) после этого получается следующее: 17 - 1 = 16, 7 - 1 = 6, так как 1 деталь мы уже забрали то есть нам нужно вычесть со всех изделий эту деталь и соответственно с некачественных тоже, так как они напрямую зависят друг от друга.
3) по теореме произведения зависимых событий, где нужно 2 события перемножить, из которых одно предполагаемое (первое событие), а второе условное идёт за ним в дальнейшем. Формула P (AB) = P (A) x P (B), где A и B - события .
Відповідь:
4,5 см
Покрокове пояснення:
Маємо паралелепіпед, в основі якого лежить ромб ABBCD;
A
C = 8 см і D
B = 5 см діагоналі паралелепіпеда;
AA
= BB
= CC
= DD
= 2 см – висота паралелепіпеда.
Висота паралелепіпеда перпендикулярна до площини основи (ромба ABCD), а значить і перпендикулярна до кожного відрізка, що лежить в площині ромба, тому AA
⊥AC і DD
⊥BD.
Звідси слідує, що трикутники A
AC і D
DB – прямокутні (∠A
AC = 90° і
∠D
DB = 90°).
Розглянемо прямокутні трикутники A
AC (∠A
AC = 90°) і D
DB (∠D1DB = 90°).
В них відомо: A
A = DD
= 2 см – катети, A
C = 8 см і D
B = 5 см – гіпотенузи відповідних прямокутних трикутників.
За теоремою Піфагора знайдемо два інших катети трикутників A
AC і
D
DB: (див. на 1-ше прикріплене фото)
Розглянемо ромб ABCD з діагоналями AC = 2√15 см і BD = √21 см.
За властивістю ромба:
діагоналі ромба перпендикулярні (AC⊥BD) і в точці перетину діляться навпіл (AO = OC = √15 см і BO = OD = √21/2 см).
Отже, трикутник AOB – прямокутний (∠AOB = 90) з катетами AO = √15 см і BO = √21/2 см.
За теоремою Піфагора знайдемо гіпотенузу AB – сторону основи паралелепіпеда (ромба ABCD):
AB² = AO² + BO² (дивись на 2-ге прикріплене фото)
Отже, AB = BC = CD = AD = 4,5 см – сторона основи паралелепіпеда.