Периметр ромба равен 200 см.
Пошаговое объяснение:
Диагональ ромба делит его высоту, проведенную из вершины тупого угла, на отрезки длиной 25 см и 15 см. Найдите периметр ромба.
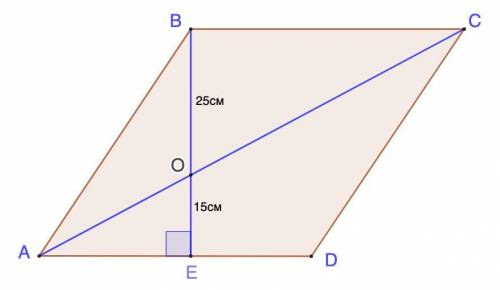
Дано: ABCD - ромб;
ВЕ - высота;
АС - диагональ;
ВЕ ∩ АС = О;
ВО = 25 см; ОЕ = 15 см.
Найти: Р(ABCD).
1. Рассмотрим ΔАВЕ - прямоугольный.
Диагонали ромба являются биссектрисами его углов.⇒ АО - биссектриса.
Биссектриса треугольника делит противоположную сторону треугольника на два отрезка, длины которых пропорциональны соответствующим прилежащим сторонам треугольника.⇒
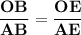 или
или 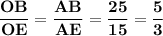
Пусть АВ = 5х см, тогда АЕ = 3х см.
ВЕ = 25 + 15 = 40 см.
По теореме Пифагора:
АВ² - АЕ² = ВЕ²
25х² - 9х² = 1600
16х² = 1600
х² = 100
х = 10 (см)
⇒ АВ = 5х = 50 см.
2. Найдем периметр ромба.
У ромба все стороны равны.Периметр ромба равен сумме длин его сторон.⇒ Р(ABCD) = AB · 4 = 50 · 4 = 200 (см)
Периметр ромба равен 200 см.
а) 5/9.
б) 1 8/11.
в) 7/15.
г) 37/ 3300.
Пошаговое объяснение:
•Чтобы обратить простую периодическую дробь в обыкновенную дробь, надо записать в числителе ее период , а в знаменателе столько девяток, сколько цифр в периоде.
•Чтобы обратить смешанную периодическую дробь в обыкновенную дробь, надо из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числитель.
А в знаменателе нужно поставить число , которое содержит столько девяток , сколько цифр в периоде, со столькими нулями справа, сколько цифр между запятой и первым периодом.
решение на фото