1) Сколькими можно в группе из 21 студента выбрать старосту, заместителя старосты,физорга.
Старостой может быть выбран любой из 21 студентов,
заместителем - любой из оставшихся 20, а физоргом – любой из оставшихся 19 студентов, т.е. 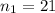 ,
, 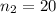 ,
, 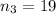 . По правилу умножения общее число выбора старосты,
. По правилу умножения общее число выбора старосты,
его заместителя и физорга равно
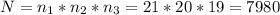
2) Порядок поступлений 9 участников конкурса определяется жеребьевкой.Сколько вариантов жеребьевки при этом возможно.
Число перестановок
9!=9*8*7*6*5*4*3*2*1=362 880
3) В семье 2 детей.Найти вероятность того, что старший ребенок мальчик.
Варианты детей в семье ММ, МД, ДМ, ДД.
Вероятность определяется по формуле
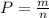
где m- количество благоприятных событий
n- всего событий
В нашем случае m=2, n=4
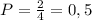
4) в урне 4 белых и 6 черных шаров, из урны по очереди извлекают 2 шара.Найти вероятность того, что вынутые шары 1 цвета.
Решение
Решим задачу решается применив формулу классической вероятности.
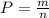
m - число благоприятных событий
n - число всех возможных событий
Для этого определим в начале число всех возможных событий n равных числу выбрать два шара из десяти имеющихся
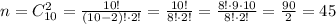
Далее определим число m - число благоприятных вариантов вынуть два белых и два черных шара по правилу суммы
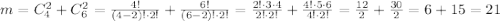
Таким образом вероятность события, что два шара одного цвета равна
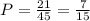
ответ: 7/15
Условие задачи на русском языке (не все числа понятны).
Прочитайте числа: 0,99; -11; 1 102; 0; -35,9. Какие из них являются: 1) отрицательными; 2) положительными; 3) неотрицательными; 4) неположительными?
0,99 - нуль целых, девяносто девять сотых;
-11 - минус одиннадцать;
1 102 - одна тысяча сто два;
0 - нуль;
-35,9 - минус тридцать пять целых девять десятых.
1) отрицательными являются числа: -11; -35,9;
2) положительными являются числа: 0,99; 1 102;
3) неотрицательными являются числа: 0,99; 1 102; 0;
4) неположительными являются числа: -11; 0; -35,9.