ответ: Пустое множество!
Пошаговое объяснение:
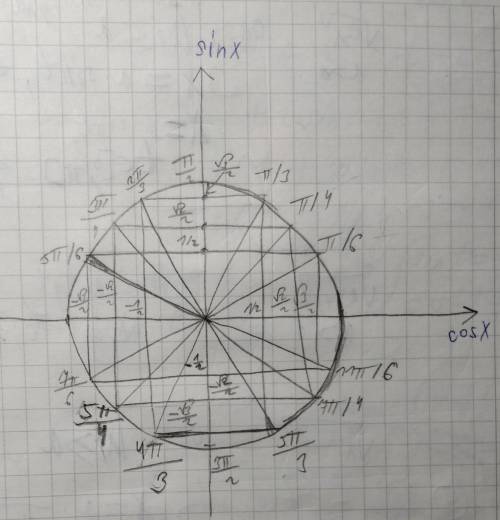
Графически (а в более сложных случаях и методом интервалов, но не в данной задаче) неравенства с тригонометрическими функциями решать как по мне наиболее удобный вариант – нужно только знать какие значения и где на окружности, если что я прикрепила свой может неаккуратный, но применимый для решения рисунок со значениями. Если что, синус угла x – ордината точки, что получена поворотом точки с координатами 1;0 вокруг начала координат на направленный угол x (направленный угол значит двигается против часовой стрелки положительный угол и по угол со знаком –)
А косинус угла х абсцисса точки, полученная аналогичным образом.
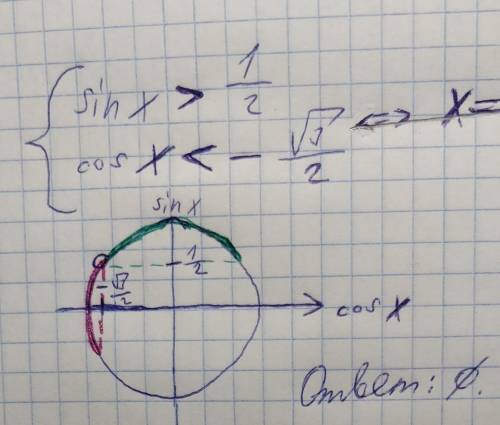
В этой задаче рисуем и получается, что единственное возможное пересечение (а так как у нас система, это и будет решением) – значение угла, чей синус равен 1/2, а косинус –√3/2, НО так как тут в системе строгие неравенства, то ответом является пустое множество.
буквенная запись- запись компонентов примера (слагаемых, суммы, делителей и т. д.) в буквенном виде.
То есть:
2+2=4 можно записать так:
a+a=b
если а-2; b-4
существует несколько законов в буквенной записи:
1.Переместительный закон: a+b=b+a
2.Сочетательный закон: (a+b)+c=a+(b+c)
3.Закон вычитания числа из суммы: (a+b)-c=(a-c)+b, где а>с
4Вычитание суммы из числа: а-(b+c)=a-b-c
5Свойство прибавления (вычитания) 0 :
a+0=a;a-0=a
Пошаговое объяснение:
Приведу пример упращения:
56+х+14
56+х+14=х+56+14=х+(56+14)=х+70
(переместительный и сочитательный законы)
Второй пример:
35-(17+х)
35-(17+х)=35-17-х=18-x
(закон вычитания суммы из числа)
Надеюсь, что объяснила более-менее понятно.
:)
а2=а1+d
a8=a1+7d
a11=a1+10d
a2+a8+a11=69
a1+d + a1+7d + a1+10d = 69
3a1 + 18d = 69
a1 + 6d = 23
a7=23