Найти разложение в степенной ряд по степеням x решения дифференциального уравнения ( записать три первых, отличных от нуля, члена этого разложения): y'=xy+2x^2 ,y(0)=0
Рассмотрим осевое сечение конуса. ΔABC - равносторонний. А - вершина конуса, BC - диаметр основания конуса. В треугольник вписан круг, это осевое сечение шара.
Пусть AH⊥BC и H∈BC. Тогда AH - высота и медина, правильного ΔABC. Поэтому H - центр основания конуса (BH=HC, середина диаметра). Значит, AH - высота конуса.
Рассмотри ΔAHC: ∠H=90°; ∠C=60°, как угол правильного треугольника; ctg C = HC/AH ⇒ HC=AH·ctg60° = AH/√3. HC - радиус конуса.
V(кон.) = h·S(осн.) = AH·π·HC² =
Радиус вписанного в правильный треугольник круга, равен трети от высоты. OH=AH/3. OH - радиус шара.
Пусть х км/ч - скорость автомобилиста, у км/ч - скорость мотоциклиста. Т к мотоциклист проезжает за 3 ч. такое же расстояние, какое автомобилист проезжает за 4ч., то 4х=3у. Отсюда у=4/3 х - скорость мотоциклиста. Пусть S километров проедет автомобилист, пока его не догонит мотоциклист, тогда мотоциклист проедет 12+S км Т к они выехали одновременно в одном направлении и мотоциклист догоняет автомобилиста, то до места встречи они проедут за одно и то же время км 36 километров проедет автомобилист, пока его не догонит мотоциклист.
км
Рассмотрим осевое сечение конуса. ΔABC - равносторонний. А - вершина конуса, BC - диаметр основания конуса. В треугольник вписан круг, это осевое сечение шара.
Пусть AH⊥BC и H∈BC. Тогда AH - высота и медина, правильного ΔABC. Поэтому H - центр основания конуса (BH=HC, середина диаметра). Значит, AH - высота конуса.
Рассмотри ΔAHC: ∠H=90°; ∠C=60°, как угол правильного треугольника; ctg C = HC/AH ⇒ HC=AH·ctg60° = AH/√3. HC - радиус конуса.
V(кон.) =
h·S(осн.) = 
AH·π·HC² =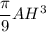 
Радиус вписанного в правильный треугольник круга, равен трети от высоты. OH=AH/3. OH - радиус шара.
V(шара) =
π·R³ = 
π·OH³ =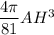 
V(шара) =
V(кон.) =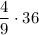 
= 4² = 16
ответ: 16.