Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -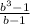
· X
После четвертой выплаты сумма оставшегося долга равна:
S4 =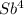 
- (1 + b +b² + b³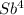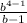)X = 
- 
· X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 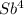- 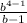· X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X = 
рублей
Решение: Запишем выражения, исходя из заданных условий: 1. К числу 650 прибавить разность чисел 530 и 210: 650 + (530 - 210) = 650 + 320 = 970. 2. Из суммы чисел 560 и 120 вычесть число 240: (560 + 120) - 240 = 680 - 240 = 440. 3. Разность чисел 650 и 210 увеличить на сумму чисел 240 и 20: (650 - 210) + (240 + 20) = 440 + 260 = 700 4. Из числа 1000 вычесть разность чисел 650 и 120: 1000 - (650 - 120) = 1000 - 530 = 470. 5. К сумме чисел 168 и 120 прибавить 240: (168 + 120) + 240 = 288 + 240 = 528.
Пошаговое объяснение:
Незнаю