1) 25,
2) 1 1/2.
Пошаговое объяснение:
1) (3 1/3 - 1 2/3) × 15 = 1 2/3 × 15 = 25
2) (5 2/5 + 9 1/6) : 9 32/45 = 14 17/30 : 9 32/45 = 437/30 : 437/45 =
= 437/30 × 45/437 = 19665/13110 = 3/2 = 1 1/2
Используем свойства ромба.
Диагонали ромба взаимно перпендикулярны, точкой пересечения делятся пополам, являются биссектрисами углов ромба.
Сумма углов, прилежащих к одной стороне ромба, равна 180°.
Значит половина диагонали 4:2=2 см;
120°:2=60°.
180°-60°=30°.
Треугольник СОД прямоугольный, с катетом 2 см и углами 60° и 30°.
Катет прямоугольного треугольника, который лежит напротив угла 30°, равняется половине гипотенузы.
CО=СД/2
2=СД/2
СД=4 - гипотенуза и сторона данного ромба.
Стороны ромба одинаковые.
Находим периметр ромба: 4+4+4+4=4*4=16 (см)
ответ: периметр ромба 16 см.
У∈[-4;5]
Пошаговое объяснение:
Чтобы найти область значений, нужно посчитать игрик от данного икс. Нам дан промежуток х∈[-2;1], значит нужно считать у(-2) и у(1) плюс вершина параболы, так как парабола - чётный график (имеет симметрию относительно Оу), и мы можем найти не минимальный игрик. Вершина высчитывается по формуле -b/2a=4/-2=-2
У нас так вышло, что край промежутка совпал с вершиной.
у=-х²-4х+1, коэффициент А отрицательный => ветви параболы направлены вниз => Унаим будет в точке 1, а Унаиб в точке -2.

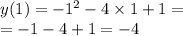
Получился промежуток от -4 до 5.
Пошаговое объяснение:
1.
1) 3 1/3 - 1 2/3 = 10/3 - 5/3 = 5/3
2) 5/3 * 15 = 75/3 = 25
2.
1) 5 2/5 + 9 1/6 = 5 12/30 + 9 5/30 = 14 17/30
2) 14 17/30 : 9 32/45 =
437/30 * 45/437 = 45/30 = 1 15/30 = 1 1/2