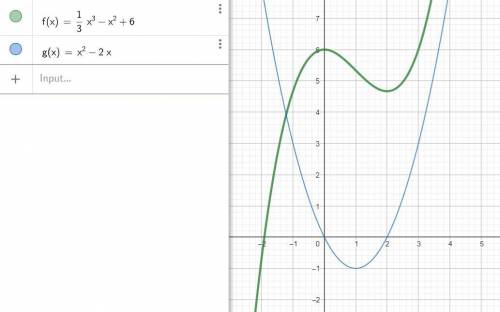
см. рис.
Пошаговое объяснение:
кубическая парабола,
снизу-вверх,
сплюснутая по вертикали в 3 раза
Взять производную,
исследовать f'(x) на f'(x) < 0, f'(x) > 0
определить экстремумы.
f'(x) = x² - 2x = x(x-2)
f'(x) = 0 при
x1 = 0
x2 = 2
f'(x) = x² - 2x (роги вверх => меньше нуля - между корнями)
f'(x) < 0 при x ∈ (0; 2) => f(x) убывает
f'(x) > 0 при x ∈ (-∞; 0) ∪ (2; +∞) => f(x) возрастает
х1 = 0 - точка максимума
х2 = 2 -точка минимума
считаем точки экстремумов
f(0) = 6
f(2) = 8/3 - 4 + 6 = 2+2/3 +2 = 4+2/3
дальше строим график, если руками - то считаем точки и соединяем плавной кривой.
а)6/8 меньше 5/8, б)1 больше 1/5, с)1/4 больше 1/5, д)1 меньше 8/7
Пошаговое объяснение:
а)чем меньше числитель, тем больше дробь
б) 1 больше 1/5 потому что, чтобы дробь была больше целого или равна целому, нужно чтобы эта дробь была неправильной.
с)чем больше знаменатель, тем больше дробь
д)8/7-неправильная дробь. переводим в смешанное число и получаем 1 1/7, а 1 1/7 явно больше 1