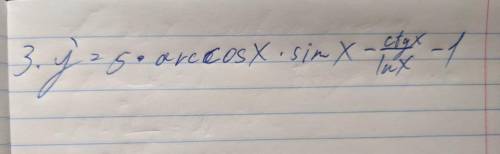
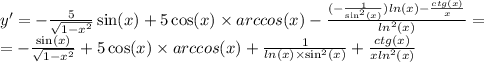
Решение проводим с калькулятора.
Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).
1) Координаты векторов
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi
здесь X,Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj
Например, для вектора AB
X = x2 - x1; Y = y2 - y1
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.6) = 53.130
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:
Найдем проекцию вектора AB на вектор AC
5) Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:
По формуле получаем:
6) Деление отрезка в данном отношении
Радиус-вектор r точки A, делящий отрезок AB в отношении AA:AB = m1:m2, определяется формулой:
Координаты точки А находятся по формулам:
Уравнение медианы треугольника
Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
M(0;-1)
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(2;1) и М(0;-1), поэтому:
или
или
y = x -1 или y -x +1 = 0
7) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
или
или
y = 3x -5 или y -3x +5 = 0
Уравнение прямой AC
или
или
y = 1/3x + 1/3 или 3y -x - 1 = 0
Уравнение прямой BC
или
или
y = -x -1 или y + x +1 = 0
8) Длина высоты треугольника, проведенной из вершины A
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:
Найдем расстояние между точкой A(2;1) и прямой BC (y + x +1 = 0)
9) Уравнение высоты через вершину C
Прямая, проходящая через точку M0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Данное уравнение можно найти и другим Для этого найдем угловой коэффициент k1 прямой AB.
Уравнение AB: y = 3x -5, т.е. k1 = 3
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим :
3k = -1, откуда k = -1/3
Так как перпендикуляр проходит через точку C(-1,0) и имеет k = -1/3,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = -1, k = -1/3, y0 = 0 получим:
y-0 = -1/3(x-(-1))
или
y = -1/3x - 1/3
Уравнение биссектрисы треугольника
Найдем биссектрису угла A. Точку пересечения биссектрисы со стороной BC обозначим М.
Воспользуемся формулой:
Уравнение AB: y -3x +5 = 0, уравнение AC: 3y -x - 1 = 0
^A ≈ 530
Биссектриса делит угол пополам, следовательно угол NAK ≈ 26.50
Тангенс угла наклона AB равен 3 (т.к. y -3x +5 = 0). Угол наклона равен 72
^NKA≈ 1800 - 720 = 1080
^ANK ≈ 1800 - (1080 + 26.50) ≈ 45.50
tg(45.50) = 1
Биссектриса проходит через точку A(2,1), используя формулу, имеем:
y - y0 = k(x - x0)
y - 1 = 1(x - 2)
или
y = x -1
как я понял
Поместное войско — обобщающее название дворянской поместной конницы, составлявшей ядро Вооружённых сил Русского государства (Русское войско, Рать) в конце XV — первой половине XVII веков.
Комплектовалась всеми служилыми людьми в государстве, московскими и городовыми, которые несли военную службу лично и бе составляя поместную дворянскую конницу
Помещики вооружались сами и вооружали своих людей за свой счёт.
Тактика поместной конницы была основана на скорости и сформировалась под азиатским влиянием в середине XV века. «Всё, что они делают, нападают ли на врага, преследуют ли его или бегут от него, они совершают внезапно и быстро. При первом столкновении они нападают на врага весьма храбро, но долго не выдерживают, как бы придерживаясь правила: Бегите или побежим мы.» — писал о русской коннице Герберштейн. Первоначально её основной целью являлась защита православного населения от набегов, главным образом, тюркских народов. В связи с этим несение береговой службы стало важнейшей задачей ратных людей и своеобразной школой их боевой подготовки. В связи с этим основным оружием конницы был лук, а оружие ближнего боя — копья и сабли — играли второстепенную роль. Русская стратегия отличалась стремлением избежать крупных столкновений, которые могли бы привести к потерям; отдавалось предпочтение различным диверсиям из укреплённых позиций.
Помимо долгого сбора, поместное войско имело ряд других недостатков. Одним из них было отсутствие систематического военного обучения, что отрицательно сказывалось на его бое Вооружение каждого человека оставалось на его усмотрение, хотя правительство давало рекомендации на этот счёт. В мирное время помещики занимались сельским хозяйством и участвовали в регулярных смотрах, на которых проверялось их вооружение и боеготовность. Другим важным недостатком была неявка на службу и бегство с неё — «нетство», которое было связано с разорением поместий или с нежеланием людей участвовать в определённой войне (например из-за несогласия с политикой правительства).