
1.
Чтобы определить количество корней, можно в уме вычислить дискриминант. Если D > 0 - уравнение имеет два корня, если D = 0 - один корень, D < 0 - не имеет корней.
а) 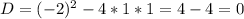
Один корень
б) 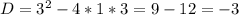
Нету корней
в) 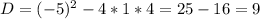
Два корня
2.
a)
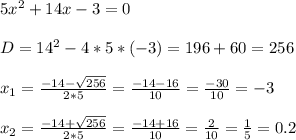
б)
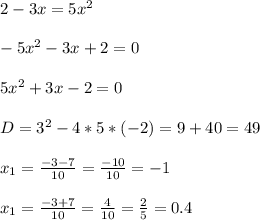
в)
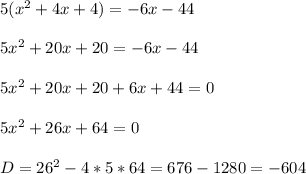
x ∈ ∅
г)
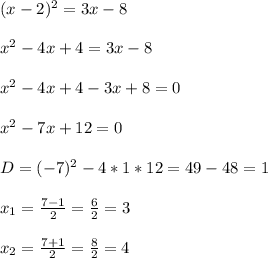
д)
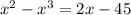
ответ: lim xn=ln2.
Пошаговое объяснение:
Так как n≠0, то выражение 2^(1/n), а вместе с ним и выражение xn=n*[2^(1/n)-1], определены при любом натуральном n. Для нахождения предела последовательности положим 1/n=m. Тогда n=1/m, при n⇒∞ m⇒0 и выражение примет вид: (2^m-1)/m. Если m⇒0, то 2^m-1⇒0 и мы имеем неопределённость вида 0/0. Для нахождения её предела используем правило Лопиталя: (2^x-1)'=(2^x)*ln2, x'=1, поэтому искомый предел равен пределу выражения (2^x-1)'/x'=(2^x)*ln2 при x⇒0. Очевидно что этот предел равен ln2.
1. а-1
б-2
в-1
2. а) х1=-3, х2=1/5
б) х1=-1, х2=2/5
в)
г) х=4
д) х=15