

при
0+ = -∞
0- = ∞
Пошаговое объяснение:
В данном решении будем пользоваться правилом произведения пределов и выделим функции
f(x) = 9x - 9
g(x) = 1/10 * x
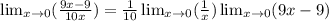
далее вычислим самый правый предел в 0, т. к. он точно существует
9 * 0 - 9 = -9
теперь наше выражение выглядит так:
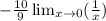
у 1/x есть асимптота y = 0 и предела двустороннего предела в 0 не существует
тогда вычислим пределы слева и справа
Пусть существует точка M > 0 и δ = 1/M тогда:
для 0+ имеем выражение 1/x > 1/(1/M) = M для всех 0 < x < δ
для 0- имеем выражение -1/x > 1/(1/M) = -M для всех -δ < x < 0
откуда получаем:
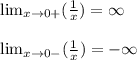
теперь полученные значения подставим в основное выражение:
-9/10 * (-∞) = ∞
-9/10 * ∞ = -∞
В решении.
Пошаговое объяснение:
Разложить на множители:
1) у⁵ - у³ - у² + 1 =
нужно так группировать члены выражения, чтобы "остатки" в скобках были одинаковыми:
= (у⁵ - у³) - (у² - 1) =
во вторых скобках знак плюс меняется на минус, так как перед скобками минус:
= у³(у² - 1) - (у² - 1) =
в изменённом выражении новый общий множитель (у² - 1):
= (у² - 1)(у³ - 1) =
первую скобку можно разложить, как разность квадратов, а вторую скобку как разность кубов:
= (у - 1)(у + 1)(у - 1)(у² + у + 1)=
два множителя (у - 1) объединить в квадрат разности:
=(у - 1)²(у + 1)(у² + у + 1).
2) 7х - ху + 7у - х² =
= (7х + 7у) - (х² + ху) =
= 7(х + у) - х(х + у) =
= (х + у) (7 - х).