a∈(-3/4; 1/2)
Пошаговое объяснение:
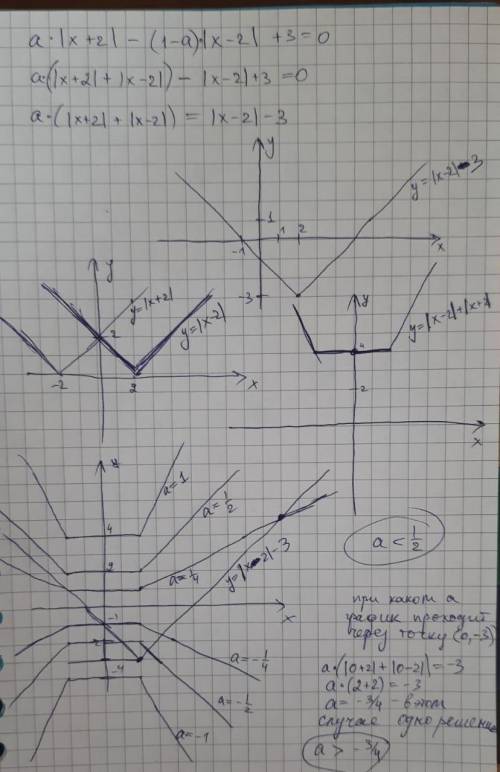
Прилагаю фото решения. Наверху преобрахование уравнения - уравниваю двае функции:
y₁=a(|x+2|+|x-2|)
y₂=|x-2|-3
Первый график - график y₁
Второй график - график вс для построения y₂ - график слагаемых |x+2| и |x-2|
Третий график - график y₂ в случае a=1
Четвертый график - изображение y₁ и разные варианты y₂, при разных значениях параметра а
а=1, а=1/2, а=1/4, а=-1/4, а=-1/2, а=-1 (при а=0 y₂ с осью Ox)
В случае a=1/2 крылья графика y₂ параллельны крыльям графика y₂ - значит они не пересекутся. (соответственно, решений не будет)
Как только мы сделаем a меньше, чем 1/2, наклон y₂ будет более пологий, чем у крыльев y₁ и значит крылья пересекутся - справа будет одно пересечение прямых и слева одно - значит будет два решения (например, смотри график при а=1/4
Теперь, каким может быть минимальное значение параметра а? (рассматриваем далее только значения a<1/2.)
В случае, который разбираю внизу справа на фото - это случай, когда вершина графика y₁ совпадет с правым углом y₂ - решаю уравнение и нахожу, что это происходит при а=-3/4 - в этом случае будет одно решение (x=2)
для всех больших значениях параметра решения будет два.
99 = 9 * 11
признаки деления
на 9 - сумма цифр, из которых состоит число, должна делится на 9
на 11 - суммы цифр. стоящих на четных или нечетных местах, должны быть равны или отличатся на 11
пусть x y две цифры
x86420y 0 <= x, y <= 9 0<= x+y <=18
1. x + 8 + 6 + 4 + 2 + y + 0 = x + y + 20
признак деления на 9 сумма кратна 9 тогда x+y = 7 или x+y = 16
2. рассмотрим признак деления на 11
x + 6 + 2 + y = 8 + 4 + 0 или x + 6 + 2 + y = 8 + 4 + 0 + 11
x + y + 8 = 12 или x + y + 8 = 23
x + y = 4 или x + y = 15
В первом случае сумма x+y=7 или 16 во втором 4 или 15
Таких цифр НЕТ
1) -11/25= -0,44
2) -21/-28= 3/4= 0,75