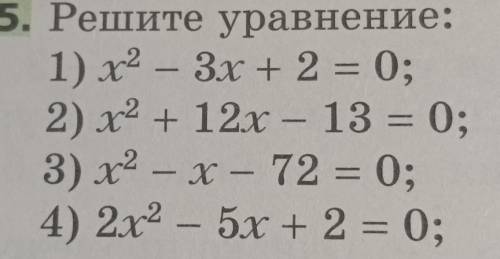
1) х^2-3х+2=0
х^2-х-2х+2=0
х(х-1)-2(х-1)=0
(х-1)(х-2)=0
х-1=0
х-2=0
х=1
х=2
х1=1; х2=2
2) х^2+12х-13=0
х^2+13х-х-13=0
х(х+13)-(х+13)=0
(х+13)(х-1)=0
х+13=0
х-1=0
х=-13
х=1
х1=-13; х=1
3) х^2–х-72=0
х^2+8х-9х-72=0
х(х+8)-9(х+8)=0
(х+8)(х-9)=0
х+8=0
х-9=0
х=-8
х=9
х1=-8; х2=9
4) 2х^2-5х+2=0
2х^2-х-4х+2=0
х(2х-1)-2(2х-1)=0
(2х-1)(х-2)=0
2х-1=0
х-2=0
х=1/2=0,5
х=2
х1=0,5; х2=2
Решение 1 задачи:
1) 40 : 10 = 4 (п.) – разложил повар на каждую тарелку;
ответ : 4 пирожка
Условие 2 обратной задачи:
Повар разложил на каждую из тарелок по 4 пирожка. Сколько пирожков он всего разложил, если тарелок было 10?
Решение 2 обратной задачи:
1) 4 × 10 = 40 ( п.) – всего было;
ответ : 40 пирожков
Условия 3 обратной задачи:
Повар взял 40 пирожков и разложил их по 4 штуки на каждую из тарелок. Сколько было тарелок?
Решение 3 обратной задачи:
1) 40 : 4 = 10 (т.) – было ;
ответ : 10 тарелок
Сделай этот ответ лучшим
1) 2(3x + 1) - x ≤ 3(x + 4), 2) 7x + 4(x - 2) > 6(1 + 3x),
6х + 2 - х ≤ 3х + 12, 7х + 4х - 8 > 6 + 18x,
5х + 2 ≤ 3х + 12, 11x - 8 > 6 + 18x,
5х - 3х ≤ 12 - 2, 11x - 18x > 6 + 8,
2х ≤ 10, -7x > 14,
х ≤ 5, x < - 2,
х ∈ (-∞; 5]; x ∈ (-∞; -2);
3) 2(x - 1) - 3(x + 2) < 6(1 + x), 4) 7(y + 3) - 2(y + 2) ≥ 2(5y + 1),
2x - 2 - 3x - 6 < 6 + 6x, 7y + 21 - 2y - 4 ≥ 10y + 2,
-x - 8 < 6 + 6x, 5y + 17 ≥ 10y + 2,
-x - 6x < 6 + 8, 5y - 10y ≥ 2 - 17,
-7x < 14, -5y ≥ -15,
x > -2, y ≤ 3,
x ∈ (-2; +∞); y ∈ (-∞; 3].
Пошаговое объяснение:
1) x²-3x+2=0
D=b²-4ac=9-4×1×2=1
x1=2
x2=1
2)x²+12x-13=0
D=b²-4ac=144-4×1×(-13)=196
x1=1
x2=-13
3)x²-x-72
D=b²-4ac=1-4×1×(-72)=289
x1=9
х2=-8
(те же формулы, что и выше)
4)2х²-5х+2=0
D=b²-4ac=25-4×2×2=9
x1=2
x2=0,5