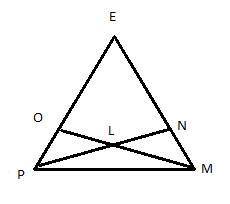
Дано:
△EPM, EO = EN = 5 см; EP = EM = 6 см.
Доказать:
а) PN = MO
б) LP = LM, где L - точка пересечения отрезков PN и MO.
Доказательство:
ЕР = ЕМ (по условию), следовательно △EPM - равнобедренный и ∠ЕРМ = ∠ЕМР. РО = ЕР - ЕО = 6-5 = 1 см. MN = EM - EN = 6-5 = 1 см, следовательно PO = MN. У треугольников OPL и NLM общая сторона PM, то PO = MN и ∠EPM = ∠EMP, то △POM = △NPM (по двум сторонам и углу между ними), следовательно PN = MO. ∠LPM = ∠LMP, следовательно △PLM - равнобедренный, значит LP = LM. Чтд.
P = 22,6 см
Пошаговое объяснение:
Периметр - это сумма длин всех сторон
У прямоугольника их 4 значит P = a + b + c + d
Зная, что у прямоугольника стороны попарно равны имеем:
P = 2(a+b)
Подставляем при а = 6,3
b = 5
P = 2(6,3+5) = 2 · 11,3 = 22,6 см
Відповідь:
P = 22,6 см
Покрокове пояснення:
Периметр-це сума довжин всіх сторін
У прямокутника їх 4 значить P = A + b + c + d
Знаючи, що у прямокутника сторони попарно рівні маємо:
P = 2(a+b)
Підставляємо при а = 6,3
b = 5
P = 2(6,3+5) = 2 · 11,3 = 22,6 см
ответ: 1) (x – 23) · 14 = 56
х-23=56:14
х-23= 4
х=23+4
х=27
(27-23)•14=56
56=56
2) 205:(у-27)=41
у-27=205:41
у-27=5
у= 27+5
205:(32-27)=41
41=41
3) 89•(b+13)=7120
b+13=7120:89
b+13=80
b=80+13
b=93
89•(93+13)=7120
7120=7120
Пошаговое объяснение:
Пошаговый ответ:
Представим треугольники EOM и ENP.
а) Так как EO = EN, а EP = EM, то вышеупомянутые треугольники EOM и ENP равны по первому признаку(угол ∡E для треугольников общий, смежные с ним стороны EP и EN соответственно равны сторонам EM и EO).
Значит стороны MO и PN равны.
б) Так как ΔEOM = ΔENP(это мы подтвердили выше), значит ∠EPN = ∠EMO. В задаче указано, что EP = EM. Значит треугольник EPM равнобедренный, и углы ∡P и ∡M равны.
Теперь, зная, что ∡P = ∡M и ∠EPN = ∠EMO, можно с уверенностью сказать, что ∠MPN = ∠PMO. Значит треугольник PML равнобедренный, значит, LP = LM.