Задача ВУЗ, надежность По данным выборки объема 9 найден доверительный интервал для оценки
математического ожидания нормально распределенного признака генеральной
совокупности: 25,38 < m < 34,84. Найти надежность полученной интервальной оценки,
если известно, что «исправленное» выборочное среднее квадратическое отклонение
равно 6.
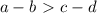
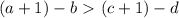
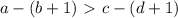
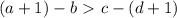
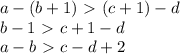
Всего есть 4 варианта увеличить числа: a и с, a и d, b и с, b и d.
Если увеличить числа а и с, то неравенство останется таким же с той лишь разницей, что к обоим частям прибавили по 1, истинность неравенства это не меняет.
Аналогично, при увеличении чисел b и d обе части неравенства уменьшатся на единицу, но истинность неравенства останется такой же.
Если увеличить числа а и d, то левая большая часть станет еще большей, а правая меньшая часть станет еще меньше, таким образом, неравенство станет еще строже и останется истинным.
Соответственно увеличивали числа b и c:
Действие аналогично прибавлению 2 к правой части и именно оно изменило истинность неравенства