Question

Как сделать оба 7. От точки М к прямой а проведены перпендикуляр МО и наклонные
MN и МК. Найдите длины наклонных AB и AC, если MO=6 см,
zNMO=60°, MN+MK=26 см.
1,
8. От точки Ак прямой а проведены перпендикуляр АО и наклонные
AB и AC. Найдите длины наклонных AB и AC, если ZC=60°,
AO=11 см, АВ – АС=7 см.

Answer 1

Пошаговое объяснение:

Answer 2

Пошаговое объяснение:

ЗАДАНИЕ 7

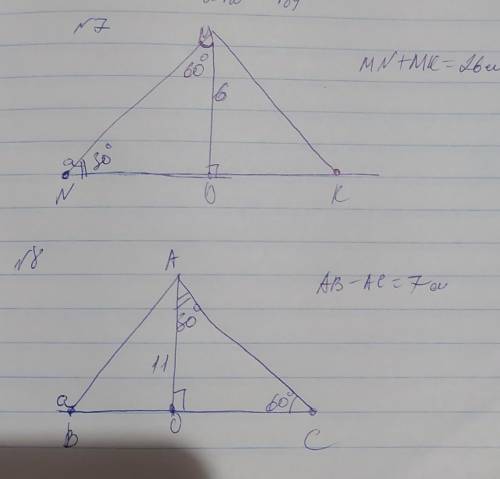
Перпендикуляр МО образует с прямой и наклонными 2 прямоугольных треугольника NMO и KMO, в которых наклонные являются гипотенуза и, а перпендикуляр и прямая - катеты. Рассмотрим ∆NMO. <NMO =60°- по условиям и так как сумма острых углов прямоугольного треугольника составляет 90°, тогда <N=90–60=30°

Катет МО, лежащий напротив угла 30° равен половине гипотенузы NM, поэтому MN=MO×2=6×2=12см.

Поскольку MN+MK=26см, то МК=26–MN=26–12=14см

ответ: MN=12см, МК=14см

ЗАДАНИЕ 8

Аналогично условиям в задаче 7: ∆ВАО и ∆САО - прямоугольные. Рассмотрим ∆САО, и если <С=60°, тогда найдём гипотенузу АС через синус угла С:

$АС= \frac{АО}{ \sin(С) } = \frac{11}{ \sin(60°) } =11÷ \frac{√3}{2} =11× \frac{2}{√3} = \frac{22}{√3}$

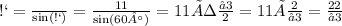
Поскольку АВ–АС=7, тогда АВ=7+АС=

$= 7 + \frac{22}{ \sqrt{3} } = \frac{7 \sqrt{3} + 22}{ \sqrt{3} } = \frac{ \sqrt{3}(7 \sqrt{3} + 22) }{ \sqrt{3} \times \sqrt{3} } = \frac{7 \times 3 + 22 \sqrt{3} }{3} = \frac{21 + 22 \sqrt{3} }{3}$

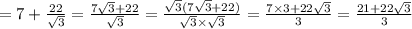
Можно так и оставить, но если нужно вычислить, то √3≈1,73, тогда:

$\frac{21 + 22 \times 1.73}{3} = \frac{21 + 38.06}{3} = \frac{59.06}{3} = 19.69$

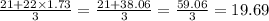
ответ: АВ≈19,69, АС=22/√3