Пошаговое объяснение:
а) Найдем сумму двух сторон прямоугольника, высоты и основания
48 : 2 = 24 см
Найдем высоту прямоугольника
(24 - 4)/2 = 10 см
б) Найдем меньшую сторону
(54-2*5)/4=11 см
Найдем большую сторону
11 +5= 16 см
в)Обозначим высоту - х см, тогда основание х+6 см
Переведем периметр в одинаковые единицы измерения
36 дм= 360 см (1дм= 10 см) Тогда согласно формуле периметра имеем
2*(х+х+6)=360
4х+12= 360
4х= 348
х= 87 см высота
x+6= 87+6 =93 cм основание
Расставим в ряд n единиц и n+1 нулей каким-то образом. Докажем, что количество таких расстановок равно количеству требуемых расстановок. Действительно, если мы добавим после каждой единицы (кроме последней) нуль, то будет выполняться требуемое условие, а если мы удалим из требуемой расстановки по нулю после каждой единицы (это можно сделать, так как ни после какой единицы не стоит единица, следовательно, после всех единиц (кроме последней) стоит нуль), получим расстановку, из которой начинали. Таким образом, получается биекция.
расставить в ряд n единиц и n+1 нулей будет (2n+1)! / (n! * (n+1)!), так как всего элементов 2n+1, при этом n и n+1 идентичных соответственно.
ответ: (2n+1)! / (n! * (n+1)!).
На 96%.
Пошаговое объяснение:
РЕШЕНО МУДROSTПусть х - это одна сторона квадрата.
Мы знаем что периметр квадрата это сумма длин всех его сторон.
Если одна сторона равна "х", то периметр равен:
Р квадрата = х+х+х+х= 4х
Площадь квадрата это произведение двух его сторон (независимо каких, потому что у него все стороны равны):
S квадрата =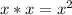 
В условии нам сказали:
"На сколько процентов увеличится площадь квадрата если его периметр увеличится на 40%?"
Переводим 40% в дробь:
40%=40:100=0,4.
Увеличиваем периметр на 40% (0,4) :
4х*0,4=1,6х (см)-на столько увеличится периметр.
А нам нужно узнать размер периметра, при увеличении на 40%, мы уже нашли эти 40%, поэтому нам нужно к периметру, который был изначально (до его увеличения на 40%) прибавить 40%, мы их уже нашли (1,6х):
4х+1,6х=5,6х (см)-периметр после его увеличения на 40%.
Теперь мы с периметра сможем найти одну сторону, раз у квадрата все стороны (4) равны, то нам нужно периметр (5,6х) разделить на количество сторон (4):
5,6х:4=1,4х (см)-это одна сторона этого квадрата (после увеличения его периметра на 40%).
Итак, мы знаем одну сторону квадрата, у которого увеличили периметр на 40%. Теперь мы можем найти площадь увеличенного квадрата.
Ещё раз повторяю что площадь квадрата это произведение двух его сторон (независимо каких, потому что у него все стороны равны):
S квадрата =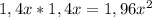 
-это площадь увеличенного квадрата.
Теперь из большей площади квадрата(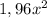 
) вычитаем меньшую площадь квадрата (
):
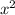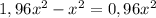
Переведём дробь в проценты:
0,96*100=96%
Значит на 96% увеличится площадь квадрата если его периметр увеличится на 40%.
РЕШЕНО МУДROST
Пошаговое объяснение: