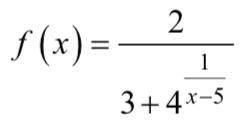
Пошаговое объяснение:
1) 0,3х-0,6=0,6+0,2х+0,8
0,3х-0,6=1,4+0,2х
0,3х-0,2х=1,4+0,6
0,1х=2
х=20
2) Сначала было в первой бочке 3х литров, а во второй х
Затем, когда начали переливать получилось в первой бочке 3х-78 л, а во второй х+42 Составим уравнение
3х-78=х+42
3х-х=78+42
2х=120
х=120:2
х=60 л было во второй бочке
60*3=180 л было в первой бочке
стало в первой бочке 180-78=102 л
стало во второй бочке 60+42=102 л
3)
4) Пусть скорость автомобиля равна х км/ч,
тогда скорость автобуса равна х-26 км/ч.
За 5 часов автобус пройдёт путь равный 5(х-26) км,
а автомобиль за 3 часа пройдёт 3х км.
По условию это одно и то же расстояние.
Составляем уравнение:
5(х-26)=3х
5х-130=3х
5х-3х=130
2х=130
х=130:2
х=65 (км/ч)- скорость автомобиля
х-26=65-26=39 (км/ч) - скорость автомобиля
5)
Сумма не должна превосходить 36. Это значит, p + q(p и q - последовательные нечётные числа) ≤36. Найду эти числа, воспользовавшись методом перебора. Выпишу те пары последовательных первых и вторых нечётных чисел, сумма которых не превышает 36. Это пары:
(1;3),(3;5),(5;7),(7;9),(9;11),(11;13),(13;15),(15;17),(17;19).
Далее читаю вторую часть условия. На основании второго условия, сумма второго и третьего удвоенного нечётных чисел не должна быть больше 49. Произведу отбор тех чисел из приведённых пар, которые удовлетворяют этому условию.То есть произведу выборку таких пар(p;q)(p-второе нечётное число, q - третье) из вышеперечисленных, что p + 2q≤49. Этому условию удовлетворяют следующие пары:
(3;5);(5;7);(7;9);(9;11);(11;13);(13;15);(15;17), поскольку 3,5,7,9,11,13,15 могут быть вторыми нечётными числами исходя из первого условия. Таким образом, только эти пары чисел могут удовлетворять приведённым двум условиям. Теперь оценим значение первого нечётного числа. Я вижу что в большинстве случаев вторые нечётные числа могут быть в роли первых предполагаемых. Значит, первое нечётное число может быть равно 3;5;7;9;11;13;15 по логике вещей. Вот такая задача )
Пошаговое объяснение:
fx=2/2 я так думаю если не правилно извините