внешний на крест
лежащий углы
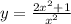 ;
;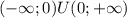 ;
;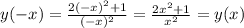 ;
;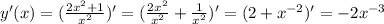 ;
; ;
;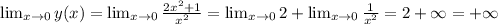 ;
; ;
;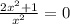 ;
;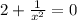 ;
;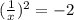 – что невозможно ни при каких действительных значениях аргумента;
– что невозможно ни при каких действительных значениях аргумента; :
: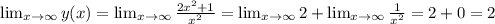 ;
; – положительна при отрицательных значениях аргумента и отрицательна при положительных х ;
– положительна при отрицательных значениях аргумента и отрицательна при положительных х ;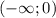 и убывает на
и убывает на  ;
;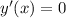 т.е.
т.е.  – не имеет решений, а значит, у функции нет экстремумов, т.е. конечных локальных минимумов или максимумов.
– не имеет решений, а значит, у функции нет экстремумов, т.е. конечных локальных минимумов или максимумов. ;
;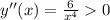 при любых значениях аргумента ;
при любых значениях аргумента ;
Внешние накрест лежащие углы