117 страниц прочитано.
Пошаговое объяснение:
1. 3 - 1 = 2 (части) на столько частей прочитано больше, чем осталось прочитать.
2. 78 : 2 = 39 (страниц) в одной части.
3. 3•39 = 117 (страниц) книги прочитано.
ответ: 117 страниц.
Проверим полученный результат:
117 стр. - прочитала девочка
117:3 = 39 (стр.) осталось прочитать
117 - 39 = 78 (стр.) на столько страниц прочитано больше, чем осталось прочитать.
Верно, условия задачи выполнены.
Схема может выглядеть так, как это сделано в прикреплённом изображении.
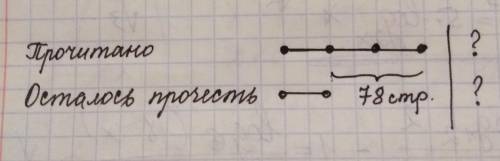
75°
Пошаговое объяснение:
По условию считаем, что каждый друзей видит свой участок стены и друзья вместе они контролируют только четвертую часть стены комнаты, что означает 90° (рисунок приложен). По обозначению эта стена дуга ВЕ = дуга ЕС + дуга СВ = 90°.
Угол обзора одного из друзей ∠CDE=10°, а у другого ∠ВАС=20°, а их сумма ∠ВАС+∠CDE=10°+20°=30°.
Нужно определить градусную меру щели КМ, т.е. дуги КМ.
Применим следующую теорему о секущих:
Угол между двумя секущими, проведенными из одной точки, равен полу разности большей и меньшей высекаемых ими дуг.
Тогда ∠ВАС=(дуга СВ - дуга КМ)/2 и ∠CDE=(дуга ЕС - дуга КМ)/2.
Поэтому
∠ВАС+∠CDE=(дуга СВ - дуга КМ)/2+(дуга ЕС - дуга КМ)/2=
=(дуга ЕС + дуга СВ - 2·дуга КМ)/2=(90°-2·дуга КМ)/2
или же
(90°-2·дуга КМ)/2=30°
90°-2·дуга КМ = 60°
2·дуга КМ = 150°
дуга КМ = 150° : 2 = 75°
1.
\begin{gathered} < var > \\y=e-\ln x\\ y'=-\frac{1}{x}\\ < /var > \end{gathered}
<var>
y=e−lnx
y
′
=−
x
1
</var>
2.
\begin{gathered} < var > \\y=\ln(10-5x)\\ y'=\frac{1}{10-5x}\cdot-5\\ y'=\frac{-5}{10-5x}\\ y'=\frac{-5}{5(2-x)}\\ y'=\frac{1}{x-2} < /var > \end{gathered}
<var>
y=ln(10−5x)
y
′
=
10−5x
1
⋅−5
y
′
=
10−5x
−5
y
′
=
5(2−x)
−5
y
′
=
x−2
1
</var>
3.
\begin{gathered} < var > \\y=3-4\ln (1-x)\\ y'=-4\cdot\frac{1}{1-x}\cdot(-1)\\ y'=-\frac{4}{x-1} < /var > \end{gathered}
<var>
y=3−4ln(1−x)
y
′
=−4⋅
1−x
1
⋅(−1)
y
′
=−
x−1
4
</var>
4.
\begin{gathered} < var > \\y=\ln \frac{1}{x}\\ y'=\frac{1}{\frac{1}{x}}\cdot(-\frac{1}{x^2})\\ y'=-\frac{x}{x^2}\\ y'=-\frac{1}{x} < /var > \end{gathered}
<var>
y=ln
x
1
y
′
=
x
1
1
⋅(−
x
2
1
)
y
′
=−
x
2
x
y
′
=−
x
1
</var>
5.
\begin{gathered} < var > \\y=1-3^x\\ y'=-3^x \ln 3 < /var > \end{gathered}
<var>
y=1−3
x
y
′
=−3
x
ln3</var>