Одна сторона треугольника равна 8 см а 2 14 см какую наименьшую длину может измерить третья сторона этого треугольника

👇

Увидеть ответ

Ответ:

dizendorfsergei007

27.01.2023

Равенство треугольника: любая сторона должна быть меньше сум двоих остальных:

8+6.1>14

ответ:6,1 см

P.S: кто не совсем точно, ведь ета сторона должна быть больше 6, а значит и 6.01см и 6.001см и т. д. тоже будут верными. Если нужно целое число, тогда будет 7см

4,5(10 оценок)

Открыть все ответы

Ответ:

Fhh72

27.01.2023

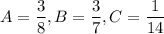
$A=\dfrac{3}{8}, B=\dfrac{3}{7}, C=\dfrac{1}{14}$

Пошаговое объяснение:

Всего вариантов последовательно выбрать три карточки: 8 * 7 * 6 (вытянули одну из восьми — осталось семь — затем осталось шесть).

A) Карточка с цифрой 1 может быть вытянута первой, второй или третьей. Тогда в каждом случае осталось семь карточек, а затем шесть: 1 * 7 * 6 + 7 * 1 * 6 + 7 * 6 * 1 = 3 * 7 * 6. Вероятность 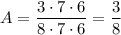$A=\dfrac{3\cdot 7\cdot 6}{8\cdot 7\cdot 6}=\dfrac{3}{8}$

B) Чётная карточка может быть вытянута первой, второй или третьей, чётных цифр всего 4 (2, 4, 6, 8). Значит, существует четыре варианта вытянуть чётную карточку, затем остаётся четыре нечётных, затем — три нечётных. То есть подходящих вариантов 4 * 4 * 3 + 4 * 4 * 3 + 4 * 3 * 4 = 4 * 4 * 3 * 3. Вероятность 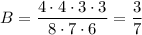$B=\dfrac{4\cdot 4\cdot 3\cdot 3}{8\cdot 7\cdot 6}=\dfrac{3}{7}$

С) Сначала вытянули одну из четырёх нужных карточек, затем — одну из оставшихся трёх, затем — одну из оставшихся двух. Нужных вариантов: 4 * 3 * 2. Вероятность 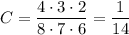$C=\dfrac{4\cdot 3\cdot 2}{8\cdot 7\cdot 6}=\dfrac{1}{14}$

4,4(48 оценок)

Ответ:

Ксюнька1801

27.01.2023

a = 9

Пошаговое объяснение:

При a < 0 уравнение не имеет корней, так как значение модуля неотрицательно.

При a = 0 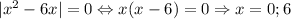$|x^2-6x|=0\Leftrightarrow x(x-6)=0 \Rightarrow x=0;6$ — два корня.

При a > 0:

$\displaystyle |x^2-6x|=a\Leftrightarrow \left [ {{x^2-6x=a} \atop {x^2-6x=-a}} \right. \left [ {{x^2-6x-a=0} \atop {x^2-6x+a=0}} \right.$

Дискриминант первого уравнения: 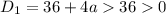D_1=36+4a360

Первое уравнение в силу ограничений на a всегда имеет два корня.

Дискриминант второго уравнения: D_2=36-4a

Второе уравнение может иметь два, один или ноль корней.

Если второе уравнение имеет два корня, то один из них должен совпадать с корнем первого уравнения. Это возможно при 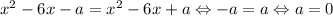$x^2-6x-a=x^2-6x+a \Leftrightarrow -a=a\Leftrightarrow a=0$ . При данном a исходное уравнение, как выяснилось ранее, имеет только два корня.

Если второе уравнение имеет один корень, то он не должен совпадать с корнем первого. Один корень уравнение имеет при дискриминанте, равном нулю: 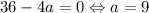$36-4a=0\Leftrightarrow a=9$ . Корень однозначно не совпадёт, поскольку совпадение произойдёт только при a = 0.