45°
Пошаговое объяснение:
Итак, из условия нам дано 2 равнобедренных треугольника - ΔABC (AB=AC) и ΔKFC (KF=FC). Углы при основании равнобедренного треугольника равны т.е. ∠ABC=∠BCA и ∠FKC=∠KCF. Также условие предлагает нам прямоугольный треугольник ΔAKF. Обозначим искомый угол ∠KCB за ∠x. Из равнобедренности следует:
∠B=∠C
∠FKC=∠KCF
∠KFA=2∠FKC=2∠KCF (это следует из смежности угла при вершине F ΔKFC с ∠KFA т.е. ∠KFA равен сумме углов при основании треугольника ΔKFC. Но Углы при основании этого треугольника равны, значит, ∠FKC+∠KCF=2∠FKC=2∠KCF)
Выразим сумму углов треугольника ΔABC с полученных нами данных:
∠A+∠B+∠C=180°=(90°-2∠KCF)+2(∠x+∠KCF)=90°-2∠KCF+2∠x+2∠KCF.
2∠KCF сокращаем, получаем уравнение:
180=90+2∠x
2∠x=180-90=90
∠X=90÷2=45°
ч.т.д
С первым числом все понятно: оно заканчивается цифрой 5, поскольку любое число, заканчивающееся пятеркой, в любой степени тоже будет заканчиваться цифрой 5.
Со вторым - аналогично: любое число, заканчивающееся шестеркой, в любой степени тоже будет заканчиваться цифрой 6.
С третьим - немного сложнее. Посмотрим, какой цифрой могут заканчиваться степени числа 2017:
и т.д.. Т.е. последнии цифры степеней числа 2017 чередуются в таком порядке - 7, 9, 3, 1 - и повторяются с интервалом в 4 цифры.
Поскольку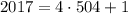
, то последняя цифра числа 
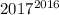- единица. Тогда последняя цифра числа 
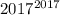- семерка.
Ну а если первое число заканчивается 5, второе - 6, третье - 7, то выражение заканчивается последней цифрой суммы последних цифр всех трех степеней: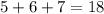
- значит, значение выражения заканчивается цифрой 8.