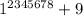| 98 - 7 + 6 - 54 - 32 - 1
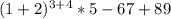| (9 + 8 * 7 * 65 + 4) * 3 - 2 * 1
в 1 ящике апельсины
во 2 ящике огурцы
в 3 ящике яблоки
в 4 ящике картофель
Пошаговое объяснение:
итак давайте начнем с 3 ящика где говорят, что здесь лежат апельсины, и мы подумаем что здесь должна быть надпись "апельсины", но нам говорят что на фруктах ложные надписи, значит это не апельсины, но здесь и овощей не будет, так как их надписи говорят правду, так что здесь лежат яблоки. Теперь смотрим 4 ящик он нам говорит, что огурцы лежат в 1 или 2 ящике, если это говорили бы огурцы то они бы лгали, но овощи говорят правду, а фрукты говорят ложь, значит здесь лежит картофель. Теперь смотрим 1 ящик здесь говорят, что во втором ящике картофель, но это не правда картофель лежит же в 4 ящике, значит это фрукт, тогда в 1 ящике лежат апельсины. Что ж теперь у нас остались огурцы и значит что эти огурцы лежат во 2 ящике, и да огурцы говорят правду яблоки не в этом ящике.
Пошаговое объяснение:
_ 9 5 4 5 | 2 3
9 2 | 4 1 5
_ 3 4
2 3
_ 1 1 5
1 1 5
0
_ 6 6 2 4 | 3 2
6 4 | 2 0 7
_ 2 2 4
2 2 4
0
Я старался печатать
Итак, для ограничения по целым степеням не более 27 по модулю, вычислимыми оказались результаты ~957 млн выводов и среди них 356 являются выводами числа 5479 и ни один вывод (а соответственно ни один вывод с операциями сложения, вычитания, конкатенации, умножения и деления, а также некоторые выводы с этими же операциями и некоторыми целыми степенями) не является выводом числа 10958. В чем его особенность?
Призраки и тени
Для задачи, аналогичной задаче Танежи в восходящем порядке, но с начальными векторами длины 8, такими как $(1, 2, ... , 8)$ и $(2, 3, ... , 9)$ количество вариантов меньше, а с иррациональными, комплексными и длинными целыми значениями элементов векторов (1) — (7) справляются оптимизированные алгоритмы Вольфрам Математики. Так, достоверно известно, что ни один вывод в $(1, 2, ... , 9)$, имеющий на 8-ой итерации оператор конкатенации, сложения или вычитания не может привести к значению 10958. Какие возможности для дальнейшего решения это даёт?
Число 10958 является полупростым. И если последняя итерация вывода не содержит сложение, вычитание и конкатенацию, то один из операндов на 8-ой итерации будет гарантировано включать 5479 в некоторой степени, за исключением двух случаев:
когда операнды кратны некоторым комплексно-сопряжённым
когда один из операндов содержит логарифм, основание или показатель которого кратны 5479