a относится к b записывается a:b или 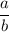
Отношение показывает, во сколько первое число больше другого
или какую часть от 2 числа составляет 1
Например 60:3 или 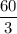 = 20
= 20
это значит, что число 60 в 20 раз больше числа 3
Не всегда всё так просто, например 2:7 уже далеко не целое число.
ответ примерно 0,29
но это отношение показывает, во сколько раз число 2 больше числа 7.
или показывает, какую часть от 7 составляет 2
Пропорция - равенство отношений.Это значит, что одно число относится ко второму так же, как третье относится к четвёртому
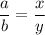
х во столько же раз больше y, во сколько раз а больше b
ну можно дополнить предыдущий пример.
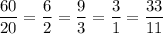
числа вроде все разные, но верхнее число всегда больше нижнего в 3 раза
Крайние и средние членызапишем пропорцию не в виде дробей
60:20=6:2
(обратите внимание: нельзя просто написать 2 отношения, поставить между ними равно и назвать это пропорцией. Частное двух чисел, то есть отношение, должно быть одинаковое, только тогда мы ставим знак = и называем это пропорцией)
Тогда члены 20 и 6 называются средними, так как они находятся ближе к знаку =
а члены 60 и 2 называются крайними, потому что они далеко от =
Очень важное свойство: произведение крайних членов равно произведению средних
и действительно: 60*2=20*6
Найти наибольшее значение её на отрезке [0;3].
Находим производную:
y' = 6x^2-18x +12 и приравниваем нулю:
6x^2-18x +12 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-18)^2-4*6*12=324-4*6*12=324-24*12=324-288=36;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√36-(-18))/(2*6)=(6-(-18))/(2*6)=(6+18)/(2*6)=24/(2*6)=24/12=2;x_2=(-√36-(-18))/(2*6)=(-6-(-18))/(2*6)=(-6+18)/(2*6)=12/(2*6)=12/12=1.
Имеем 2 критические точки - 3 промежутка значений производной.
Находим знаки производной на этих промежутках.
x = 0 1 1,5 2 3
y' = 12 0 -1,5 0 12.
В точке х = 1 производная переходит с + на -, это точка локального максимума.
Но, как видим, после точки х = 2 функция возрастает( знак + производной).
Поэтому находим значение функции на правой границе промежутка.
х = 3, у = 2*3³-9*3²+12*3 = 54-81+36 = 9.
ответ: максимальное значение функции на заданном промежутке равно 9.