ответ:в 8 раз меньше
Пошаговое объяснение:4кг=4000г
4000:500=8(раз)
Вот и всё!
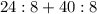
 повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение: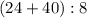
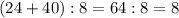 В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на
В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на  , то и их сумма делится на
, то и их сумма делится на  .
.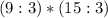
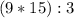
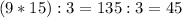
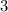 ,то их произведение делится на
,то их произведение делится на 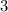 " доказанным.
" доказанным.
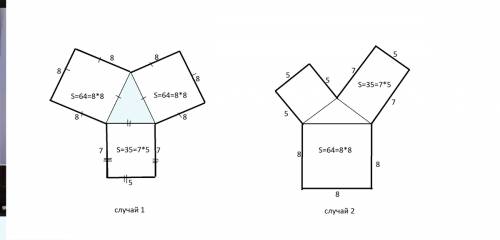
в 8 раз
нормально