Пошаговое объяснение:
Раскроем модуль в первом уравнении
-11 ≤ x+2y+1 ≤ 11, (x-a)^2 +(y-2a)^2 = 2+a
-12-x≤2y≤10-x, (x-a)^2 +(y-2a)^2 = 2+a
Получаем систему;:
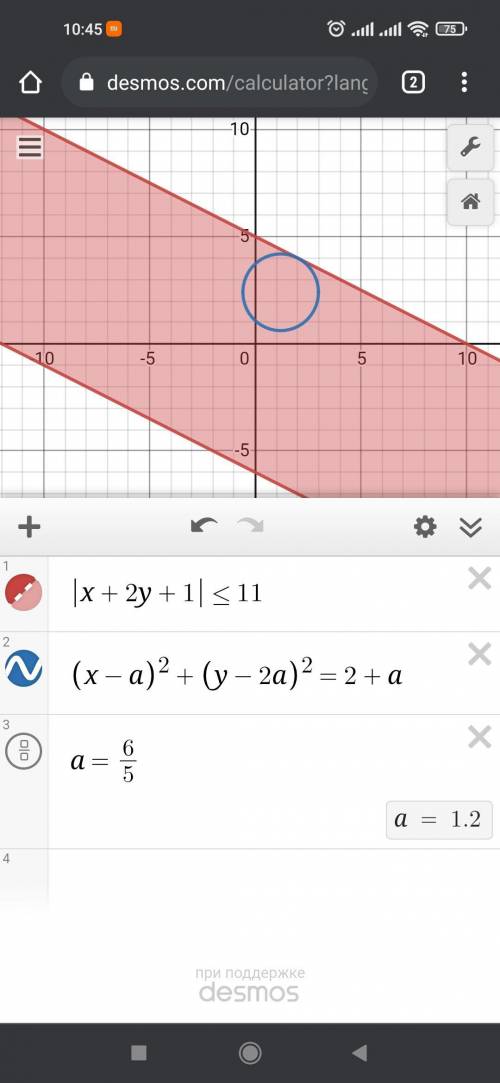
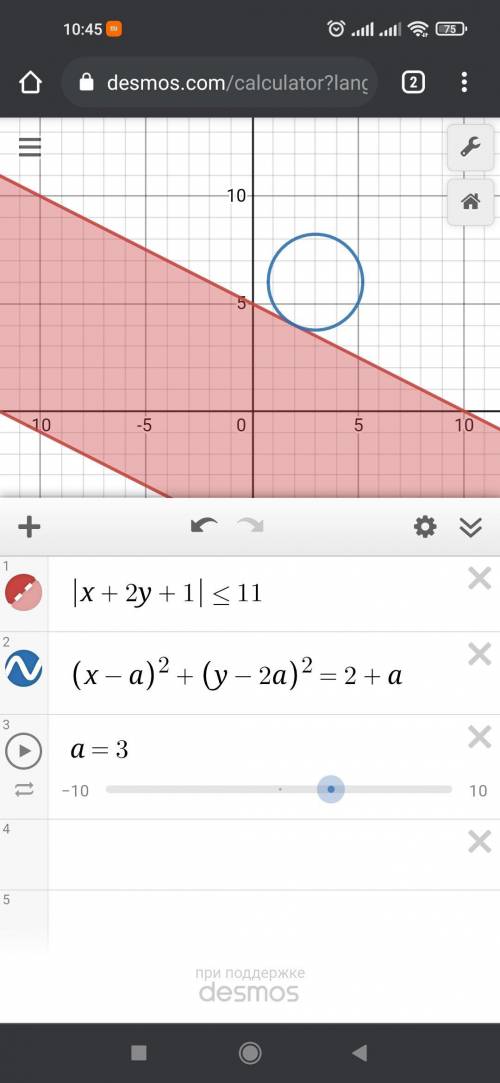
y ≥ -x/2 - 6
y≤ -x/2 +5
(x-a)^2 +(y-2a)^2 = 2+a → уравнение окружности с радиусом √(2+а) и центром в координатах (а;2а). Радиус ≥0, подставим а=-2 и найдем координаты
(х+2)^2+(у+4)^2=0. Радиус ноль, координаты точки (-2;-4), что находятся в пределах системы неравенств с прямыми. При увеличении параметра окружность будет двигаться вверх, центр будет лежать на прямой у=2х. Единственное решение будет тогда, когда окружность касается верхней прямой, тоесть 2x=-x/2 +5
5x/2 = 5, x = 2 => y =4. Подставляем в уравнение окружности. (2-а)^2+(4-2а)^2 = 2+а
Раскрываем скобки, решаем и получаем а = 3, а = 6/5. Так как для единственности решения окружность должна касаться прямой у=-х/2+5 сверху, то нам подходит большее значение параметра а=3, ответ а=3
Прибавим и отнимем 2х² в левой части уравнения:
х⁴ - 3х³ - 2х² + (- 2х² + 2х²) - 6х - 8 = 0
х⁴ - 3х³ - 4х² + 2х²)- 6х - 8 = 0
х²(х² - 3х - 4) + 2х² - 6х - 8 = 0
х²(х² - 3х - 4) + 2(х² - 3х - 4) = 0
(х² - 3х - 4)(х² + 2) = 0
1) х² + 2 = 0
х² = -2 - это невозможно
Так как х² > 0 или х² = 0
х² + 2 ≠ 0
2) х² - 3х - 4 = 0
D = 3² + 4•4 = 9 + 16 = 25
√D = √25 = 5
х1 = (3+5)/2 = 8/2 = 4
х2 = (3-5)/2 = -2/2 = -1
ответ: 4; -1.
Проверка
При х = 4
4⁴ - 3•4³ - 2•4² - 6•4 - 8 =
= 256 - 192 - 32 - 24 - 8 = 0
При х = -1
(-1)⁴ - 3•(-1)³ - 2•(-1)² - 6•(-1) - 8 =
= 1 + 3 - 2 + 6 - 8 = 0